
|
BRHS /
Hugoniot curveFor steady, one-dimensional flow of a combustible gas that burns to completion, equations relating initial and final conditions are called the Rankine-Hugoniot relations and they provide jump conditions across the front, from upstream (subscript 0) to downstream (subscript \infty ) . These equations are: 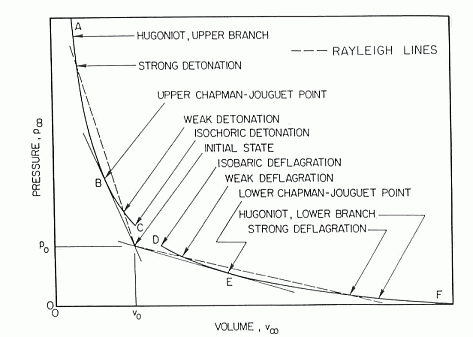 Figure 1. Schematic locus of burnt-gas states for combustion waves (LinanA:1993). m_{0} \equiv \rho _{0} u_{0} =\rho _{\infty } u_{\infty } P_{0} \equiv \rho _{0} u_{0}^{2} +p_{0} =\rho _{\infty } u_{\infty }^{2} +p_{\infty } The sequence of final states obeying p_{\infty } +m_{0}^{2} /\rho _{\infty } =P_{0} \equiv p_{0} +m_{0}^{2} /\rho _{0} obtained by substituting first two equations, is the Rayleigh line, a straight line in the plane of final pressure p_{\infty } , and specific volume, 1/\rho _{\infty } , such as Fig.1. Use of energy conservation equation together with second jump condition provides a relationship among thermodynamic properties, the Hugoniot curve, which can be written as: \left(\frac{\gamma }{\gamma -1} \right)\left(\frac{p_{\infty } }{\rho _{\infty } } -\frac{p_{0} }{\rho _{0} } \right)-\frac{1}{2} \left(\frac{1}{\rho _{\infty } } +\frac{1}{\rho _{0} } \right)\left(p_{\infty } -p_{0} \right)=h_{0} where h_{0} is the total amount of chemical heat release per unit mass of the mixture, The Hugoniot curve is shown schematically in Fig. 1 for a representative combustion system. The final state is determined by the intersection of the Rayleigh line with the Hugoniot curve. The Hugoniot curve has two branches, an upper branch of large \rho _{\infty } and p_{\infty } , called the detonation branch, and a lower branch of small \rho _{\infty } and p_{\infty } , called the deflagration branch. There is a minimum propagation velocity for detonations, corresponding to tangency at the upper Chapman-Jouget point. The Rankine-Hugoniot equations can be solved by e.g., STANJAN code, examples of results from such computations for hydrogen-oxygen and hydrogen-air mixtures are given in Table 1. Table 1. Calculated detonation properties for hydrogen mixtures with oxygen and air initially at 298 K and 1 atm (ReynoldsWC:1986).
Overdriven detonationUnder certain circumstances, it is possible for the detonation wave to move faster than the unique steady-state velocity given by CJ theory. This usually occurs because another event causes the detonation products to move faster than the velocity they would have in a CJ wave. As a result, the pressure associated with the overdriven detonation front can be significantly higher. The extent of pressure increases that can occur can be seen in Table 2 for hydrogen-air and hydrogen-oxygen detonations. Table 2. Theoretical pressure (bar) for overdriven detonation in stoichiometric hydrogen mixtures (TeodorczykA:1992).
Linan A. and Williams F.A. (1993) Fundamental Aspects of Combustion. Oxford University Press.(BibTeX) << Detonation direct initiation | Content | Chapman-Jouget detonation >> |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||