
|
BRHS /
Personnel Protective EquipmentAccidental ConsequencesContributing Authors
Pressure Waves and Pressure LoadsEssential to the consideration of accidental consequences is the estimation of hazards and hazard levels, e.g., overpressures, thermal radiation, and the estimation of the damage level or the vulnerability of the receiving objects. In chemical explosions, which are usually exothermal oxidation reactions, a great portion of the combustion energy is carried by the developing blast wave which is uniformly distributed in all directions. Depending on the various types of combustion processes (slow deflagration or fast turbulent flame or detonation), the pressure history will be different. It is characterized by the peak overpressure and the pressure increase/decay rate. This effect is strongest at ground level (hemispherical) explosions where due to reflection the respective yield ratio can be twice as high as for a spherical explosion. 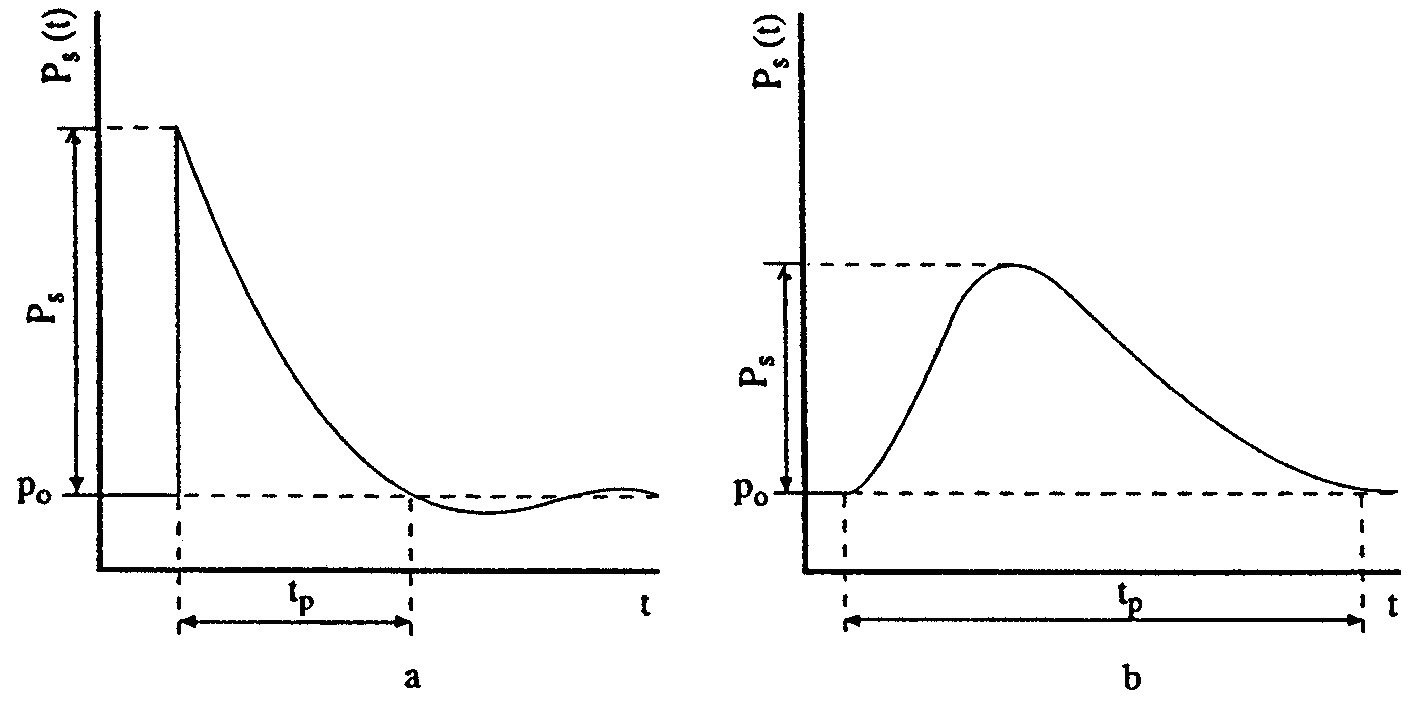 Fig. 1: Characteristic shape of pressure-time function for a detonation shock wave (left) and a deflagration pressure wave (right) (Po: initial pressure; Ps: peak side-on overpressure; tp: duration of positive phase) ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=CPR16E:2005:GreenBook | CPR16E:2005:GreenBook)]] Deflagration and detonation differ in peak overpressure, in the duration of the impulse (time-integrated pressure), in the steepness of the wave front, and in the decrease of overpressure with propagation distance. Secondary blast wave parameters are the peak reflected pressure, peak dynamic (blast wind) pressure, shock front velocity, and blast wave length. The different pressure transients for the two combustion modes are shown in Fig. 1. DeflagrationIn a deflagration with flame speeds of 1-10 m/s, the volume expansion of the gas acts like a piston displacing the unburnt gas. The deflagration pressure wave in a confined space is characterized by a slow increase of pressure and fluid velocity in the region preceding the flame front. The pressure in the vessel is independent of the location and mainly determined by the fraction of burnt gas. The static pressure loading in slow deflagration processes is described by the “adiabatic, isochoric, complete combustion” (AICC) pressure representing an upper bound in a confined space. A mitigation of the AICC pressure is given by incomplete combustion, venting, radiation/conduction heat losses, or the addition of diluents. Therefore the maximum static pressure will be generally lower than the AICC pressure. On the other hand, initial turbulence increases the degree of combustion and thus the pressure. The peak pressure in a closed vessel for most hydrocarbon mixtures is in the order of 0.8 MPa, sufficient for many buildings to exceed their failure limits. For a hydrocarbon-oxygen mixture, it is even 1.6 MPa. A hydrogen-air mixture, initially at NTP, will reach a pressure of 0.815 MPa; its volume will increase by a factor of 6.89 (BakerWE:1983). The pressure buildup depends on the flame propagation and the degree of confinement. Particularly hazardous configurations are those, which are heavily confined like tubes, pipes, or channels, where – if long enough – even in insensitive methane-air mixtures, high flame speeds and pressures can be reached. Venting can reduce the pressure. Inside a spherical vessel, the pressure rise following the ignition of a flammable mixture is proportional to the cube of the burning velocity. In pipes with no obstacles, the transition distance increases with increasing diameter (example: 8 m for propane-air mixture in a 50 mm diameter pipe) (MoenIO:1993). The effective burning velocity must be as high as ~ 100 m/s to produce significant blast overpressures of 10 kPa. Comparing explosion tests in tubes and in spherical vessels, it was observed that pressures are generally lower in a spherical propagation of the gas mixture (unconfined) than in a planar propagation. The pressure behind the flame front is decaying away from the flame, since wave energy dissipates. The combustion of a hydrogen-air mixture in an unconfined vapor cloud explosion (UVCE) typically liberates only a fraction of 0.1-10 % of its thermal energy content, in most cases less than 1 % (LindCD:1975). Depending on the combustion mode (deflagration/detonation), the explosion is connected with a more or less destructive pressure shock wave. Fast DeflagrationIn the intermediate stage of a fast deflagration with the flame front still traveling at subsonic speed, a preceding shock wave is developing in the still unburnt mixture. The peak overpressure is lower, the pressure drop, however, takes place over a longer period of time. This means that the impulse, i.e., the integral of pressure over time, which is a measure for the load upon a structure, is about the same in both cases. The peak overpressure increases with increasing flame speed. Transient pressures can be locally higher than the AICC pressure. Inhomogeneities can result in local detonations decaying to deflagrations. When the shock wave leaves the cloud, it turns into an expanding decaying wave. In the long-distance range, the pressure wave for both deflagration and detonation exhibits about the same shape decaying with 1/r. Local explosions like from jet flames result in locally high pressures and can also result in high flame speed in less confined areas and may even trigger a detonation wave. DetonationIn contrast, the detonation is a combustion mode with the flame traveling at supersonic speeds in the order of 2000 m/s. The flame front proceeds by shock wave compression of the unburnt gas. It is characterized by a distinct pressure spike and a subsequent almost exponential decrease. The shock wave, which is at the same time the flame front, is followed by the reaction zone, in which a pressure discontinuity is observed where the pressure even drops to values lower than atmospheric pressure (“molecular collapse”) due to the much denser oxidation product (water) upon hydrogen combustion. The essential parameters are peak overpressure and positive/negative phase of the specific impulse depending on the liberated explosion energy. The combustion process is completed without an expansion of the gas cloud. Peak overpressures in the near field are typically in the range of 1.5-2 MPa. The pressure wave gradually decays and eventually turns into an acoustic wave. In geometries which allow the transition from deflagration to detonation, pressures near the location where detonation takes place, may be much higher than the CJ (Chapman-Jouguet) pressure of a stabilized (and idealized) detonation wave, which is due to a pre-compression effect by the propagating shock wave (VanWingerdenCJM:1999). In confined spaces, peak pressures can range between “normal” deflagration peak pressure and very high pressures following DDT. Worst case is considered the DDT on a reflected shock wave produced by a fast flame with an estimated peak pressure to be by a factor of 10 higher than the detonation pressure. The transfer of a detonation wave into adjacent mixtures is possible and has been observed for planar clouds, whereas in spherical clouds, fast deflagrations are more likely to occur. An explosion in a vessel which is connected by a small opening to another vessel creates a peak overpressure and a pressure increase rate much higher than in a single vessel explosion, a phenomenon known as “pressure piling”. A pressure of more than 3.5 MPa was measured in a two-chamber geometry for a stoichiometric hydrocarbon-air mixture, where 0.8 MPa were expected for the explosion in a single vessel. Unlike the length of the interconnecting tube, its diameter is pertinent for the peak overpressure. Real Gas CloudIn reality, a gas cloud shows the typically expected features of a non-premixed, inhomogeneous concentration distribution, air entrainment at the boundaries, and stratification if evolving from a pool of liquefied gas. Furthermore in case of an explosion, a real gas cloud is not an “ideal” explosion source due to a larger-than-infinitesimal volume and a lower energy density and energy deposition rate, thus leading to non-ideal blast waves. Deviations from the ideal situation are able to either enhance or to attenuate the pressure buildup. Non-stoichiometry as well as ignition at the cloud edge will certainly have a damping effect on the pressure buildup. The maximum blast impulse, which becomes larger with increasing shock duration, is not near the explosion center, but about 13-15 charge radii. A near-ground flat long-stretched cloud of heavy gases or vaporized cryogens may experience multi-point ignition connected with a sequence of pressure peaks, and more turbulence-generating terrain roughness or obstacles in the flow path, both effects of which lead to an enhancement of the pressure buildup. Unlike a heavy gas cloud which would be of a pancake form, a hydrogen vapour cloud would soon cover an area, which is larger than that of a hemispherical cloud with the same explosive inventory. Only in case of just vaporized LH2 after a large-scale spill, the cold gas cloud would travel and stretch near ground, until sufficient air has entrained from the outside to make the gas positively buoyant and develop soon to a vertically stretched cloud shape. The flame spreading in a non-spherical cloud is spherically until it reaches the cloud edge at some point; then it continues in the direction, where still gas can be found. The pressure is decreasing immediately behind the flame front because of the upward expansion of the combustion products. Invalid BibTex Entry! Shock wave blasts can also be produced from physical explosions, i.e., the sudden violent expansion of a fluid not connected with a chemical reaction. The strongest man-made physical explosion is surely the nuclear explosion of an atomic bomb. The resulting blast wave reaches overpressures of 170 kPa in the central zone (14 km radius for the example of a 20 Mt explosion in 5.5 km height) and gradually decaying to the outside with still 20 kPa at 60 km distance). The most common physical explosion is a bursting or rocketing pressure vessel which may result from a fire-induced BLEVE (Boiling Liquid Expanding Vapor Cloud Explosion). The higher the liquid density, the more destructive is the BLEVE. If the liquid is flammable, a fireball will follow. Several pressure spikes are being created upon a BLEVE: from the flashing liquid, from the expanding vapor phase, and, if applicable, from the combustion. Missiles and projectiles may be emitted also from a physical explosion and may cause injuries, fatalities, or damage at considerable distances depending on the explosion energy liberated. Projectile hazard increases with average liquid temperature. Another example of a physical explosion is the so-called rapid phase transition (RPT), a thermal vapor explosion resulting from the spontaneous phase change of a fluid getting in contact with a much hotter or colder liquid, e.g., a cryogen spilled onto water. Prerequisites of such an explosive boiling is a temperature of the “hot” fluid above the boiling point of the “cold” fluid and a certain mixing of both fluids allowing a close and sufficiently long contact. Although the energy release is small compared with a chemical explosion, fragmentation and phase change of the “cold” fluid (vapor evolution) can occur at such a high rate that shock waves may be formed. For LNG onto a water surface, overpressures with damaging potential of up to 5 kPa were observed. RPT explosions with different materials (molten metal plus water) in the metal and chemical industries were even the cause for people killed by flying melt or the blast wave. Natural examples of RPT were the catastrophic explosions of the island volcanoes Krakatoa, Indonesia, in 1883 and Surtsey, Iceland, in 1963. 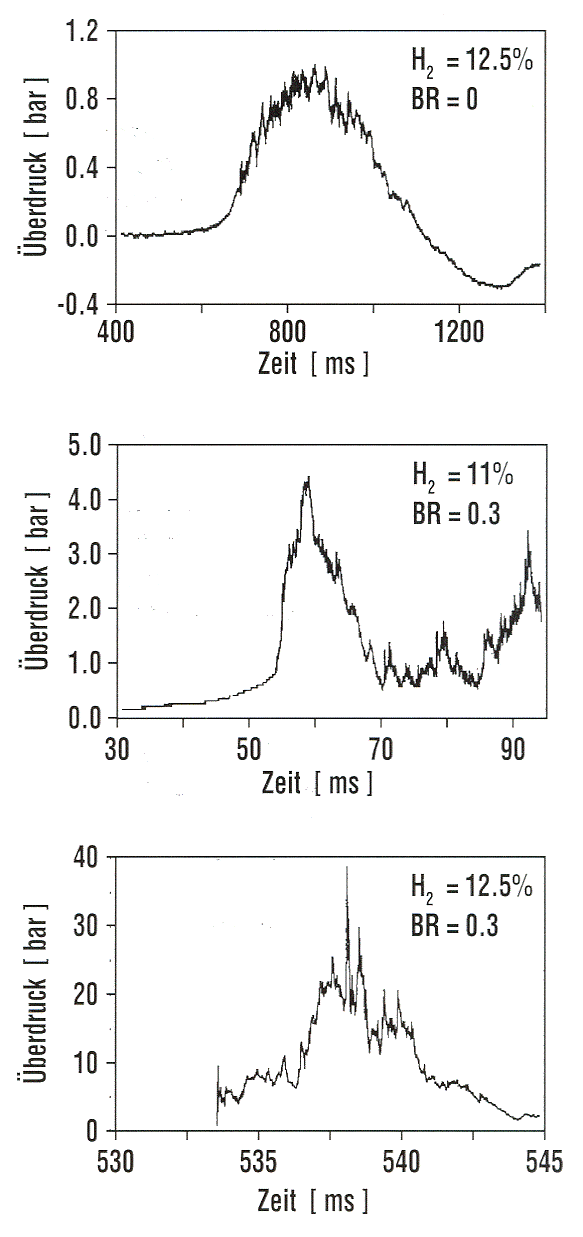 Fig. 1: Measured overpressure transients in RUT tests with different blockage ratios (BR) showing slow deflagration (top), fast deflagration (middle), detonation (bottom) ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BreitungW:1996 | BreitungW:1996)]] Apart from the experience obtained by observations and lessons learned from explosion accidents, numerous experiments have been performed worldwide to investigate the transient behavior of overpressures following the explosive combustion of fuel-air mixtures. Tests were conducted under various conditions such as confined, partially confined, or unconfined, larger-scale or smaller-scale geometry, fuel type and constitution with the main goal of development of or comparison with simulation approaches. The most dangerous configurations were found to be, as expected, those with a major obstruction, even for less sensitive fuel gases such as methane. For DDT cases, travelling distance for the flame must be sufficiently long, which would be around 3 m for a stoichiometric hydrogen-air mixture. Only a few of those test series are mentioned in the following showing the broad range of activities. Large-scale experiments were conducted by the Russian Kurchatov Institute using premixed hydrogen-air mixtures. The RUT facility with a confined volume of 480 m3 was employed for a series of tests ranging from slow deflagration to detonation. Hydrogen concentrations varied between 10 and 14 %. During slow deflagration (no obstacles present), the overpressures measured increased with H2 concentration, from around 0.1 MPa to 0.17-0.23 MPa. Insertion of obstacles (blockage ratio of 30 and 60 %) resulted in accelerated flames creating overpressures of 1.1-1.6 MPa for gas mixtures with 14 % H2 concentration. There was even the observation of a detonation at a H2 concentration as low as 12.5 % (Fig. 1). The Russian UTR facility, a tube with 66 mm diameter and a maximum length of 3 m, was used for systematic studies with gas mixtures of hydrogen, oxygen, and nitrogen. Peak overpressures and impulses were investigated as a function of the location of DDT which influences the degree of precombustion. Peak pressures observed were well above the Chapman-Jouguet pressures for detonation of the undisturbed mixture (BreitungW:1996). Large-scale testing on DDT in hydrogen-air mixtures was conducted in the FLAME facility ("Flame Acceleration Measurements and Experiments"), a 30.5 m long, 2.44 m high, and 1.83 m wide rectangular channel with a closed ignition end and an open far end and with venting/obstruction possibilities between fully closed and 50 % open. Tests were carried out with variation of H2 concentrations (12-30 vol%), obstacle blockage ratio (0-33 %), and top venting. The observed lower detonability limits were at 15 vol% of H2 with obstacles and 25 vol% of H2 without obstacles. DDT also occurred at a 24.8 vol% H2 concentration with a 13 % open top. Top venting was found to have two counteracting effects: increase of burning rate due to turbulence dominant at low venting rates, and flame speed reduction due to loss of gas for large venting rates (YangJW:1991). An explosion tube of 2.5 m diameter and 10 m length with one open end was used in Norway to study peak overpressures of ignited stoichiometric propane-air mixtures. The tests have shown the significant influence of the blockage ratio inside the tube on the flame speed and pressure increase, respectively, which can come close to the detonation range (GexCon:2006). Smaller-scale detonation test tubes have been conducted at the Research Center Karlsruhe, the Technical University of Munich, the DLR in Stuttgart or the High-Temperature Combustion Facility, HTCF, at BNL employing different types of obstruction and differently diluted hydrogen-air mixtures to study flame acceleration and various DDT mechanisms. Within the nuclear power plant safety program and the PNP gas cloud program, the German Fraunhofer Institute for Chemical Technology (FH-ICT) conducted various series of tests using mixtures of propane, ethylene, methane, and hydrogen with air to investigate detonation and DDT in spherical, hemispherical, and tube geometries. Unconfined hemisperically shaped H2-air mixtures at volumes between 7.5 and 2100 m3 were ignited measuring a maximum overpressure of 6.3 kPa which corresponds to a flame velocity of 84 m/s (SchneiderH:1978); (PfortnerH:1983); (PfortnerH:1983a); (PfortnerH:1985). Balloon tests were conducted with hemisperically shaped H2-air mixtures with a volume of 50 m3 and concentrations of 20 and 29.6 vol%, respectively. Ignition occurred at the center on the ground by means of an explosive to trigger detonation. Pressures were measured at various positions inside and outside the balloon (Figs. 2 and 3). Visually measured flame speeds agreed well the theoretical values (BreitungW:1995).  Fig. 2: Measured and calculated pressure transient inside the balloon in an FH-ICT hemispherical balloon test with H2-air detonation ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BreitungW:1995 | BreitungW:1995)]] 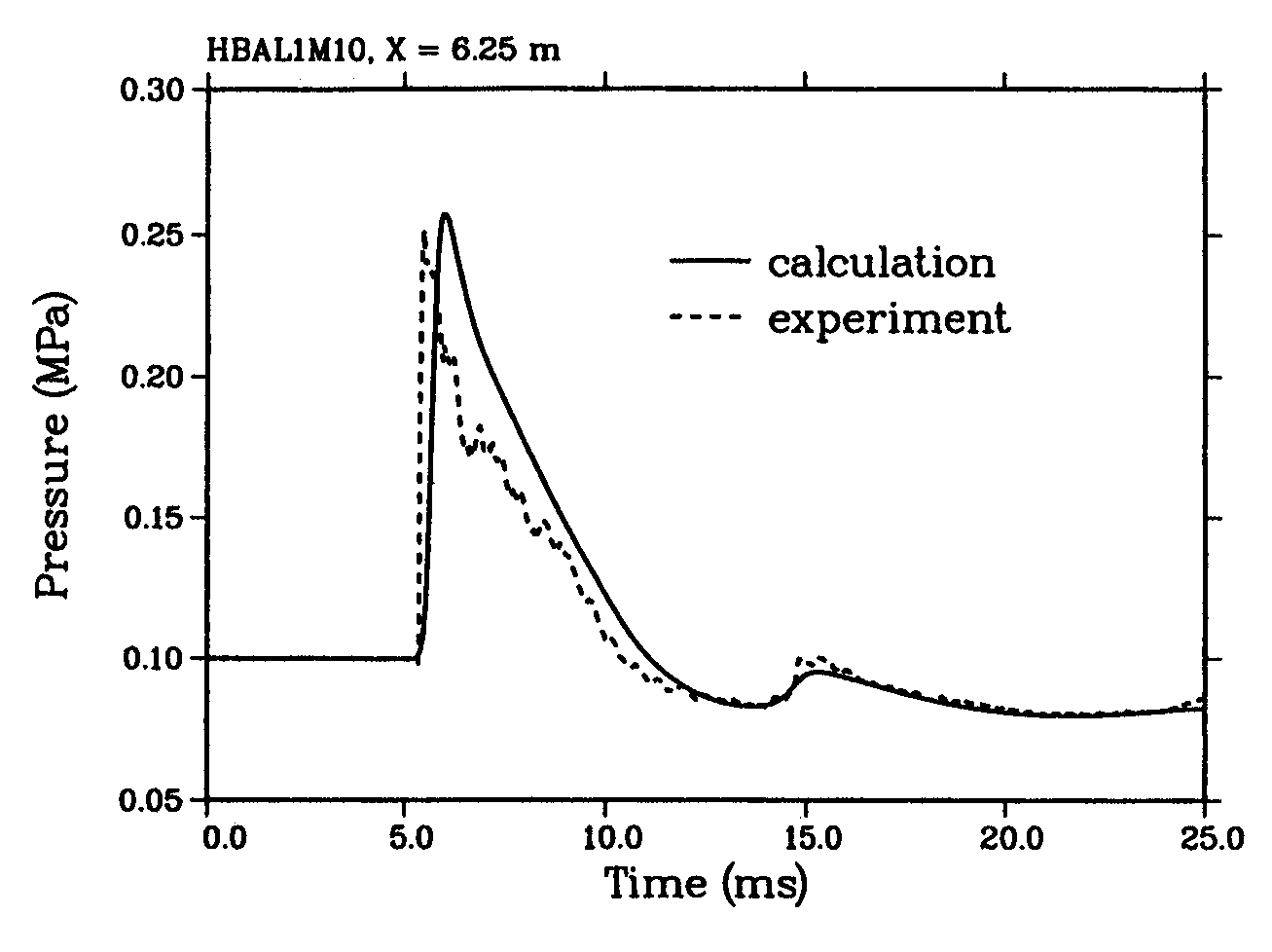 Fig. 3: Measured and calculated pressure transient outside the balloon in an FH-ICT hemispherical balloon test with H2-air detonation ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BreitungW:1995 | BreitungW:1995)]] The influence of partial confinement on the combustion behavior of H2-air mixtures was examined in further ICT tests employing a 10 x 3 x 3 m3 lane with parallel walls (PfortnerH:1983); (PfortnerH:1983a); (SchneiderH:2005), which also have resulted in one case in a transition from deflagration to detonation (Fig. 4). The extensive experimental research programs on gas explosions within the EU projects MERGE (MercxWPM:1994) and EMERGE (MercxWPM:1997) have shown that overpressures are mainly determined by fuel type, geometric scale as well as the arrangement and number of obstacles which are passed by the propagating flame. Other unconfined explosion tests are known of the BASF company in Germany. In 1943 and 1948, explosion accidents occurred at BASF resulting from the bursting of liquid gas vessels, subsequent flash evaporation, and mixing of the fuel with ambient air and eventually ignition of the cloud. The cause of the bursting was a heating of the overfilled vessels by the radiation of the sun, i.e., there was not enough vapor buffering inside of the tanks. The experimental simulation and modeling of these events has been performed in the 1970s by BASF and Fraunhofer ICT by use of differently sized vessels with volumes between 0.2 and 1.2 m3 corresponding to a mass of up to 452 kg of liquid propylene. Pressures observed were in the range of 0.5-1.5 kPa for the smaller and 4-7 kPa for the larger vessels (MaurerB:1975); (MaurerB:1977); (GiesbrechtH:1980); (GiesbrechtH:1981). With respect to other physical explosions, tests were conducted in the 1970s and 1980s with the spillage of LNG into a pond of water (e.g., Coyote series, Burro series, Maplin Sands series) to measure among other parameters the strength of RPT pressure waves. After releasing LNG amounts of 40 m3 onto water, observed RPT overpressures were as high as 5 kPa (KoopmanRP:1982). 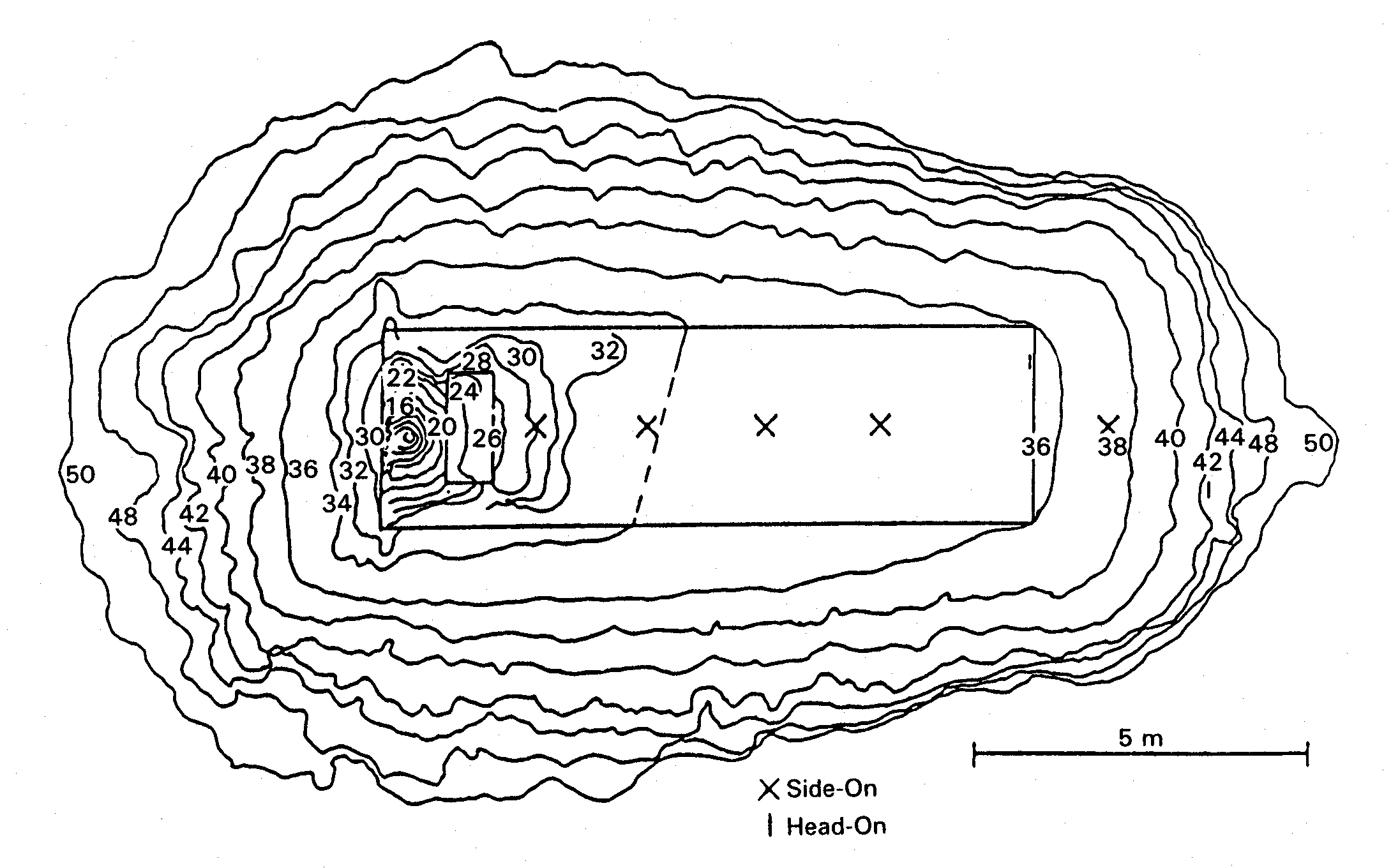 Fig. 4: Measured flame front profiles in an FH-ICT lane test with parallel walls (37 % H2 air mixture), fan generated turbulence, and DDT near the wall (contour 34) ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BermanM:1986 | BermanM:1986)]] Gaz de France initiated an RPT research program in 1981 in Lorient with large-scale tests using LNG. The spillage of amounts between 1 and 9 m3 onto water has shown that the occurrence and strength of RPT were strongly related to the volume of the mixing zone. Maximum explosion pressure recorded was equivalent to 4.15 kg of TNT. Research activities also included fundamental studies of the phenomena and computer code development. Due to the larger temperature difference, consequences of LH2 spills onto water may be more severe. Invalid BibTex Entry! The explosion energy in case of a BLEVE can be assessed by the difference between final and initial state of the bursting vessel assuming isentropic expansion. This plus a certain portion of the bursting pressure energy contribute to the blast wave generation (CSCHE:2004). The propagation of a pressure wave in a compressible medium can be described by the Rankine-Hugoniot equations (or “jump conditions”) based on the conservation equations for mass, momentum, and energy. From this relationship, it can be derived that the density ratio of air, if assumed to be an ideal gas, behind and in front of the shock front is limited to about 6. For air as a real gas, however, assuming to dissociate or ionize at high temperatures, this ratio can be significantly higher. A computer code, BLAST (Building Loads Analysis and Systems Thermodynamics), was developed based on the above equations as well as on empirical data from nuclear tests. 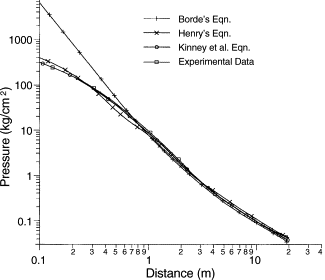 Fig. 1: Blast pressures vs. scaled distance for a detonation of 1 kg of TNT ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=PandeyAK:2006 | PandeyAK:2006)]] A first model description of the shock wave parameters for an explosion in air was given in 1870 by Rankine with shock front velocity, maximum dynamic pressure as functions of the peak static overpressure, speed of sound in air, and the atmospheric conditions. Later modelling efforts have used theoretical or empirical approaches to find agreement with experimental data (PandeyAK:2006). Fig. 1 shows a comparison of measured explosion pressures with different models. It was generally stated that agreement between theory and experiment is less good in the near-field compared to the medium and far-field because of the more complex flow pattern. Accurate empirical and theoretical models are existing for detonation waves. According to the Chapman-Jouguet (CJ) theory of 1899 and 1905, respectively, detonation represents a linear discontinuity, transforming the reactants completely to products at an infinite reaction rate. Detonation velocity and pressure can be calculated from equilibrium chemistry as a function of the gas mixture only. Respective data for hydrogen at NTP in an unsupported detonation are
The CJ theory predicts the thermodynamic state immediately behind the detonation wave, but cannot describe the structure of the wave. Processes inside the detonation front are extremely complex involving multi-dimensional shock interactions in an intensive turbulent reacting medium. Still, the simple one-dimensional CJ model prediction of velocity and overpressure is quite close to what is being observed, within a few per cent for velocity and 10-15 % difference for the pressure measurements (TieszenSR:1993). CJ (and AICC) pressures of a fixed gas mixture increase linearly with the initial pressure at constant initial temperature, and are inversely proportional to the initial temperature at constant initial pressure. However, the CJ theory is not capable of determining the dynamic detonation parameters such as detonability limits, initial energy or critical tube diameter. No theory exists so far that provides estimates of these parameters. CJ parameters of a gas or gas mixtures can be calculated with the code STANJAN developed at the Stanford University. In the ZND (Zel’dovich-von Neumann-Doering) theory, the detonation wave is described as a two-dimensional dome-shaped shock wave, where at its front both temperature and pressure rise. It is followed by a reaction zone whose thickness is determined by the reaction rate. Here the detonable substance reacts at high pressure and temperature until everything is transformed into product gases. The chemical reaction causes a rapid fall in pressure (“von Neumann spike”). The reaction zone remains unchanged (steady) when moving through the substance. A variable ranging between 0 and 1 describes the respective state and the progress of chemical reaction, respectively. Detonation velocities and pressures are less than for a plane shock front. A very simple way of modeling blast effects is the TNT Equivalent method derived from the decay of shock waves from high-explosive or nuclear explosions in the atmosphere. It is an estimation of the mass of TNT per unit mass of fuel, whose detonation would result in the same blast wave at the same distance. One kg of TNT translates into energy of 4520 kg meaning that 1 Nm3 of hydrogen gas corresponds to 2.22 kg of TNT. The weakness of the TNT Equivalent model, if applied to a vapor cloud explosion, is to ignore the pressure-time characteristic differences between a gas cloud and a detonative TNT explosion. It is deemed to overestimate near-field and underestimate far-field effects. Furthermore the model does not consider the influence of turbulence and confinement. The TNT model considers only the total amount of fuel involved and particularly does not take into account the yield factor in a vapor cloud explosion, which is generally only a small fraction, in most cases < 1 %. The most common form of blast scaling law is that according to Hopkinson and Cranz (BakerWE:1983):
where Z is the scaled distance, R is the distance from the center of explosion, E is the total heat of combustion, W is the total weight of a standard explosive (such as TNT). The law has been validated against numerous experiments over a large range of explosion energies and can be applied to predict blast wave properties of large-scale explosions based on the data of smale-scale experiments (assuming same explosive, same geometry). There is, however, a lack of experimental data at very small scaled distances; the above relation appears to become inappropriate for Z < 0.16 m/kg1/3. 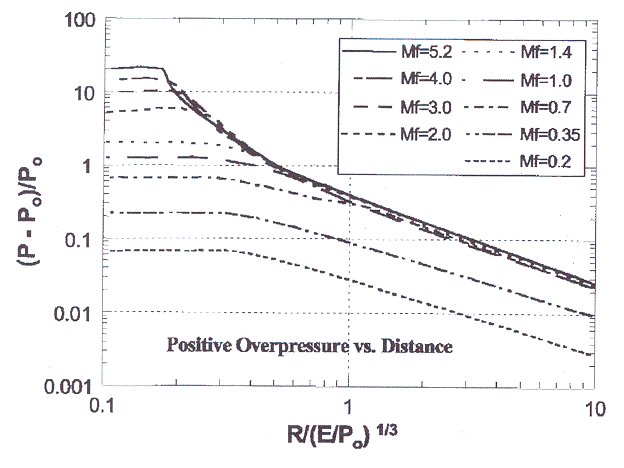 Fig. 2: Baker-Strehlow-Tang curves of overpressure vs. distance for various flame Mach numbers ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=TangMJ:1999 | TangMJ:1999)]] A wide variety of explosion experiments has been evaluated to derive blast charts. Commonly known and accepted are the Baker-Strehlow blast curves for vapor cloud explosions in the open atmosphere or the TNO blast waves for hemispherical explosions. It is a good engineering tool finding its limits when real gas clouds rather than idealized are considered. An improvement towards a more realistic modeling was made with a new set of blast curves, called the Baker-Strehlow-Tang curves (Fig. 2), by considering a more precise blast pressure decay behavior. The result is a considerable reduction at long distances. The curves were validated in all combustion regimes (TangMJ:1999). Models for BLEVE Blast prediction are also described in the CCPS guidelines (AICHECCPS:1994) and the so-called ‘Yellow Book’ of TNO (CPR14E:2005:YellowBook). These references also describe models to predict the magnitude and duration of the fireball which often follows a BLEVE. Recently a new numerical method to calculate the blast effects originating from an exploding vessel of liquefied gas have been derived (vandenBergAC:2004)(vandenBergAC:2004). Adequate blast calculation requires full knowledge of the blast source characteristics, i.e., the release and subsequent vaporization rate of the flashing liquid. As the conditions that allow explosive vaporization are not entirely clear and the vaporization rate of a flashing liquid is unknown, safe assumptions have been adopted as the starting point in the modelling. The blast effects from a BLEVE are numerically computed by imposing the vapour pressure of a flashing liquid as boundary condition for the gas dynamics of expansion. The modelling shows that the rupture of a pressure vessel containing a liquefied gas in free space only develops a blast of significant strength if the vessel near-instantaneously disintegrates.  Fig. 3: Blast overpressure vs. scaled distance for different explosion strengths according to the Multi-Energy method ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=MercxWPM:2000 | MercxWPM:2000)]] The TNO Multi-Energy method is based on the Multi-Energy concept, which consists in the feature of gas deflagration that overpressure and blast develop only under appropriate boundary conditions, i.e., only where the flammable mixture is partially confined and/or obstructed (AICHECCPS:1994)(MercxWPM:1991)(MercxWPM:2000). This assumption can be made provided that transition to detonation to DDT does not take place. For hydrogen, this requirement is not as easily fulfilled as it is for most hydrocarbons. Based on the Multi-Energy concept, a vapor cloud explosion is modeled as series of hemispherical model charges. Each model charge is characterized by a charge size and a charge strength. The charge size is related to the heat of combustion present in the source, while the charge strength is related to the explosion overpressure. Based on these characterizations, scaled blast parameters (peak overpressure, positive phase duration) as a function of scaled distance have been calculated with the TNO FCT ("Flux-Corrected Transport") Euler solver ‘BLAST’ (Fig. 3) (MercxWPM:2000). The strength of the blast wave is expressed as a number between 1 and 10 representing categories of “insignificant” to “detonative”. Calculation results suggest that damaging explosions can occur only, when flame acceleration takes place within a plant structure (MercxWPM:1991)(MercxWPM:2000). The charge strength can be determined either by numerical calculation (CFD) or by using the experimentally based GAME correlation Invalid BibTex Entry!, a relation between the overpressure and details of obstacle configurations. The charge size is influenced by the Critical Separation Distance (CSD), the distance between two obstructed regions above which a vapor cloud explosion can be modeled as two separate sources of blast. Guidance on the CSD has been obtained in experimental research projects such as RIGOS Invalid BibTex Entry!. It has been found that the CSD between a ‘donor’ and an ‘acceptor’ increases with the explosion overpressure up to a maximum of half the donor dimension. The Research Center Karlsruhe has developed the calculation models DET1D and DET3D to determine the characteristic detonation parameters within the reaction zone and outside in the unburnt mixture. These models have been mainly applied to assess the load on a nuclear containment upon confined combustion of homogeneous mixtures of H2, O2, N2, H2O. Code validation was made against the Russian RUT experiments and FH-ICT balloon tests (see Figs. 1 and 2 in previous section on "Experimental Work"). Parameter calculations of a 3D detonation have shown that the 3D structure is not important for the pressure load and that a relatively coarse grid provides sufficient accuracy (BreitungW:1995). The state-of-the-art approach to modeling of combustion phenomena are 3D CFD codes, which need to be adapted to the spatial and temporal lengths characteristic for chemical reactions. Typical time steps for hydrodynamic flow calculations are in the order of 10-6 s and for the H2-O2 reaction mechanism 10-10 s (BreitungW:1995). Many approaches are based on the assumption of incompressible flows and are restricted to slow deflagrations or to pure detonations. For fast deflagrations with Mach numbers > 0.3, incompressibility can no longer be assumed, since pressure waves are not negligible. Several methods of turbulence modelling have been developed. In the “Reynolds Averaged Navier Stokes” (RANS) equations, turbulence is modelled by means of a turbulence viscosity which can be calculated in a k-ε two-equations system. In contrast, the “Direct Numerical Simulation” (DNS) employs the direct and complete solution of the conservation equations taking into consideration all turbulent structures. Somewhere in between is the method “Large Eddy Simulation” (LES) where only the large turbulence structures are being dissolved by the calculation grid, whereas small turbulences are filtered away and covered a turbulence viscosity model approach. Today’s modeling and simulation show good agreement with a variety of fast combustion phenomena. It has the potential to provide accurate data for realistic scenarios depending on how accurately the respective submodels are working. For example, the above mentioned LES method for turbulent flows with high Reynolds numbers was successfully applied to the FH-ICT deflagration test with stoichiometric H2-air mixture (MolkovVV:2005a). The application of computer models, however, should be limited to cases or ranges, for which the codes were validated. Examples of CFD codes applied to combustion are AIXCO (RWTH, Germany), AUTOREAGAS (TNO & ANSYS Century Dynamics, The Netherlands), CFX (Harwell, UK), FLACS (CMI, Norway), FLUENT (Fluent, USA), GASFLOW (FZK, Germany), PHOENICS (CHAM, UK). Invalid BibTex Entry! No fully validated model exists in terms of predicting projectile hazards from bursting pressure vessels. However, this difficult physical problem may be divided in two parts:
The first part is probably the most complex one, and only numerical simulation seems to allow for prediction using appropriate material and fracture models as, e.g., shown in (GursonAL:1977); (ErdoganF:1977); (MottNF:1943). The second part couples beginning solicitation and ballistic considerations. Solutions as suggested in (BaumMR:1999); (BakerWE:1983); (UFIP:2002) are the most widely applied and easy-to-handle models. The software PROJEX using a method developed by INERIS may also be used and seems to give better results (INERIS:2004). A global model based on statistical considerations is also being conceived in (HauptmannsU:2001). Most modeling approaches deal with the effects of blast and fire. In many hydrogen explosion scenarios however, the throw of missiles or debris is also important and in some cases even dominant. For hydrogen gas explosions this is typically the case for scenarios where some degree of confinement or enclosure is present. When in combination the combustion process changes from a deflagration to a detonation the throw of missiles or debris can be devastating. Examples are gas explosions inside industrial equipment, inside a garage or car park, or in a nuclear plant. These scenarios may lead to a major hazard of debris or missiles. Other types of explosions involving hydrogen are BLEVE’s and physical explosions. In these scenarios, it is typically a vessel rupture leading to the throw of missiles. Any risk assessment methodology for hydrogen should contain models for the throw of debris or missiles. The Initial ConditionsIn general the initial conditions for throw are defined by the distributions of the missile or debris mass, launch velocity, and launch direction. These conditions are determined by the failure process and the subsequent acceleration by the expanding gasses, or reaction products. This is accompanied by pressure relief as a result of the increasing vent area between the accelerating items. The initial conditions for throw of missiles from vessels, as a result of physical explosions, BLEVE’s and internal gas explosions can be determined with PGS02 (CPR14E:2005:YellowBook), referred to as the ‘Yellow Book’, and the CCPS Guideline (AICHECCPS:1994). In these references, the models of Baum (BLEVE’s), Baker (physical explosions) and Gel’fand (physical explosions and internal gas explosions) are presented. For BLEVE’s, the model of Baum predicts the initial velocity of missiles based on the amount of liberated energy. The model of Baker for physical explosions relates the initial velocity of missiles to a scaled overpressure, the vessel geometry, and the number of fragments. With the model of Gel’fand for internal gas explosions, the initial velocity is based on the scaled overpressure and a scaled energy release rate. The break-up process of buildings constructed from reinforced concrete or brick during an internal gas explosion is a more complicated phenomenon. In the case of a (weak) deflagration, the combustion continues during the break-up process and debris launch. The coupling between pressure build-up, venting, and break-up determines the part of the structure that will participate in the throw, and the distributions of debris launch velocity and launch direction.  Fig. 1: Kasun storage building with an internal volume of 8 m3 (left), Result after detonation of 2 kg TNT (right) ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=LangbergH:2004 | LangbergH:2004)]] When a hydrogen detonation takes place inside a building the combustion process is completed before the structure starts to break up. As a result, the structure is loaded with a quasi-static load of typically 0.8 MPa overpressure. This by far exceeds the structural strength of any typical industrial building. As a result, the structure will largely break up and accelerate. Hydrogen detonations in buildings can be compared with bare quantities of high explosives in ammunition magazines. A similar quasi-static load is obtained when a bare charge resulting in a loading density of 0.25 kg/m3 of TNT is detonated. In Fig. 1, the result after the detonation of 2 kg of TNT in an 8 m3 Kasun-building (Norwegian "small quantities" ammunition storage building) is displayed (LangbergH:2004). 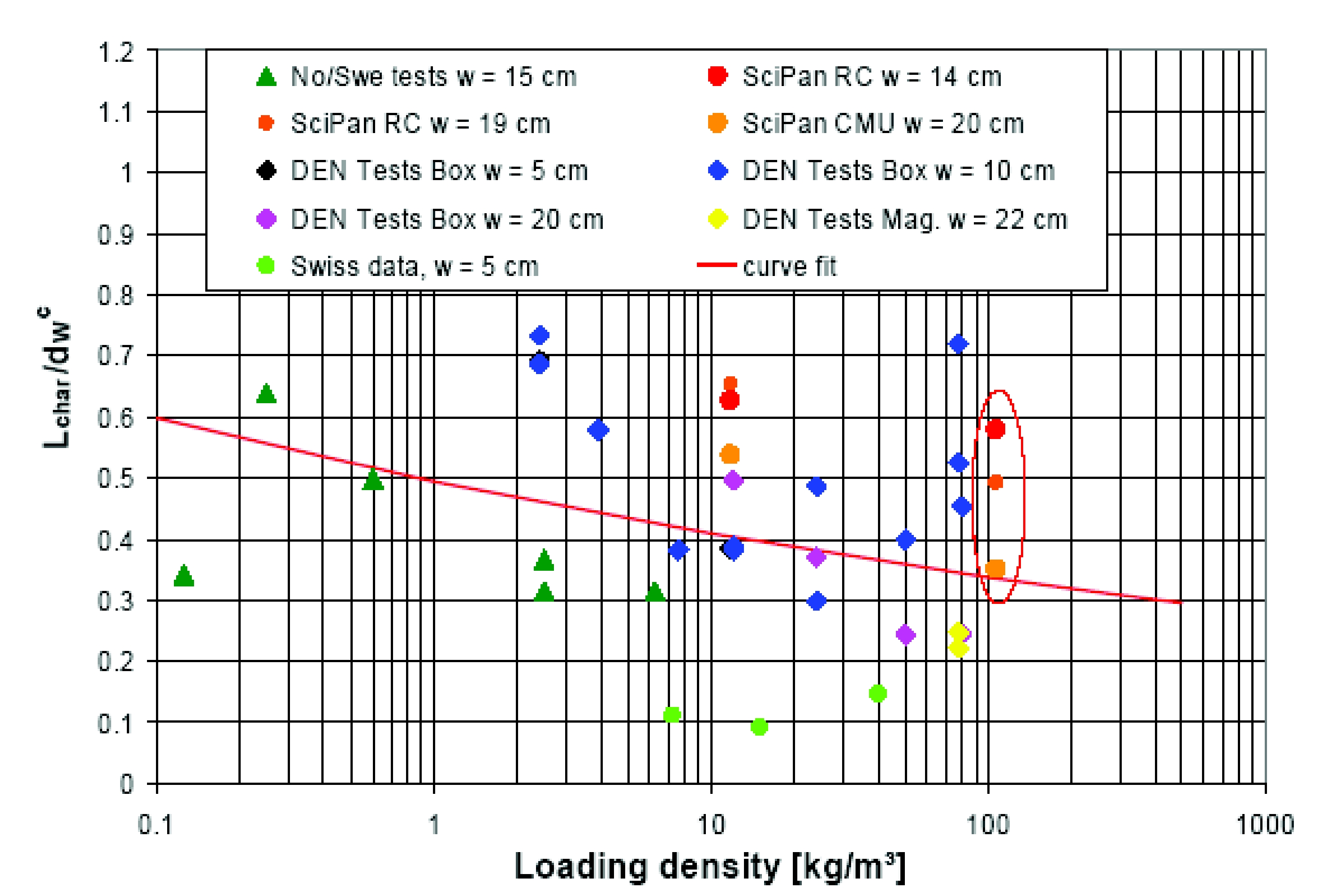 Fig. 2: Characteristic length versus loading density for the Klotz Group trial database ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=VanDoormaalJCAM:2006 | VanDoormaalJCAM:2006)]] For detonations of bare explosives in ammunition magazines, relations for the distributions of debris mass, launch velocity, and launch direction have been derived within the Klotz Group ((VanDoormaalJCAM:2006); (VanDoormaalJCAM:2006a)). Those relations are based on debris pick-up data from a collection of large scale trials, and depend on loading density and wall thickness. The cumulative debris mass distribution was found to decay exponentially with debris mass. The characteristic length of debris decreases slowly with loading density. Fig. 2 shows this characteristic length for a large collection of trial data. Note that the effective loading density for hydrogen detonations of 0.25 kg/m3 is situated at the low loading density regime of the trial database.  Fig. 3: Development of the debris throw during a Kasun trial with 50 kg TNT illustrating the strong directionality of throw The initial debris velocity decreases with debris mass around a typical velocity, the Debris Launch Velocity (DLV). This relation has been based on backward calculations. The launch angle distribution was found to be a rather sharp Gaussian distribution centered around a direction close to the wall normal directions. This directionality is illustrated in Fig. 3, where a frame is shown during the debris launch from a Kasun-building after detonation of 50 kg TNT. Note that this loading density exceeds the energy content of a hydrogen detonation by far. The addition of the new Sci Pan 3 trial to the database was recently reported (vanderVoortMM:2006). The relations are currently being implemented in a software code, the KG-Engineering Tool. The Throw of Debris and MissilesThe initial distributions are the required input for throw models. Throw models determine a collection of impact locations in the field. Together with the impact velocity and impact angle the consequences for the infrastructure and for human beings can be determined. Most existing throw models make use of a Monte Carlo technique. Predefined initial distributions of debris or missile mass, launch velocity and launch direction are sampled to obtain the initial conditions for a number of trajectory calculations. To obtain a proper representation of the debris or missile density in the field, the required number of Monte Carlo simulations needs to be very large. A global model based on statistical considerations is also being conceived in (HauptmannsU:2001). Recently TNO has developed a universal throw model (Van der Voort et al. 2006). The basis is the source function theorem, an underlying mathematical relation between the debris or missile density and the initial distributions. This model reduces the required number of trajectory calculations dramatically. Trajectory calculations have to be carried out with caution since the selected shape, orientation and drag coefficient of debris and missiles have a significant influence on throw distances. 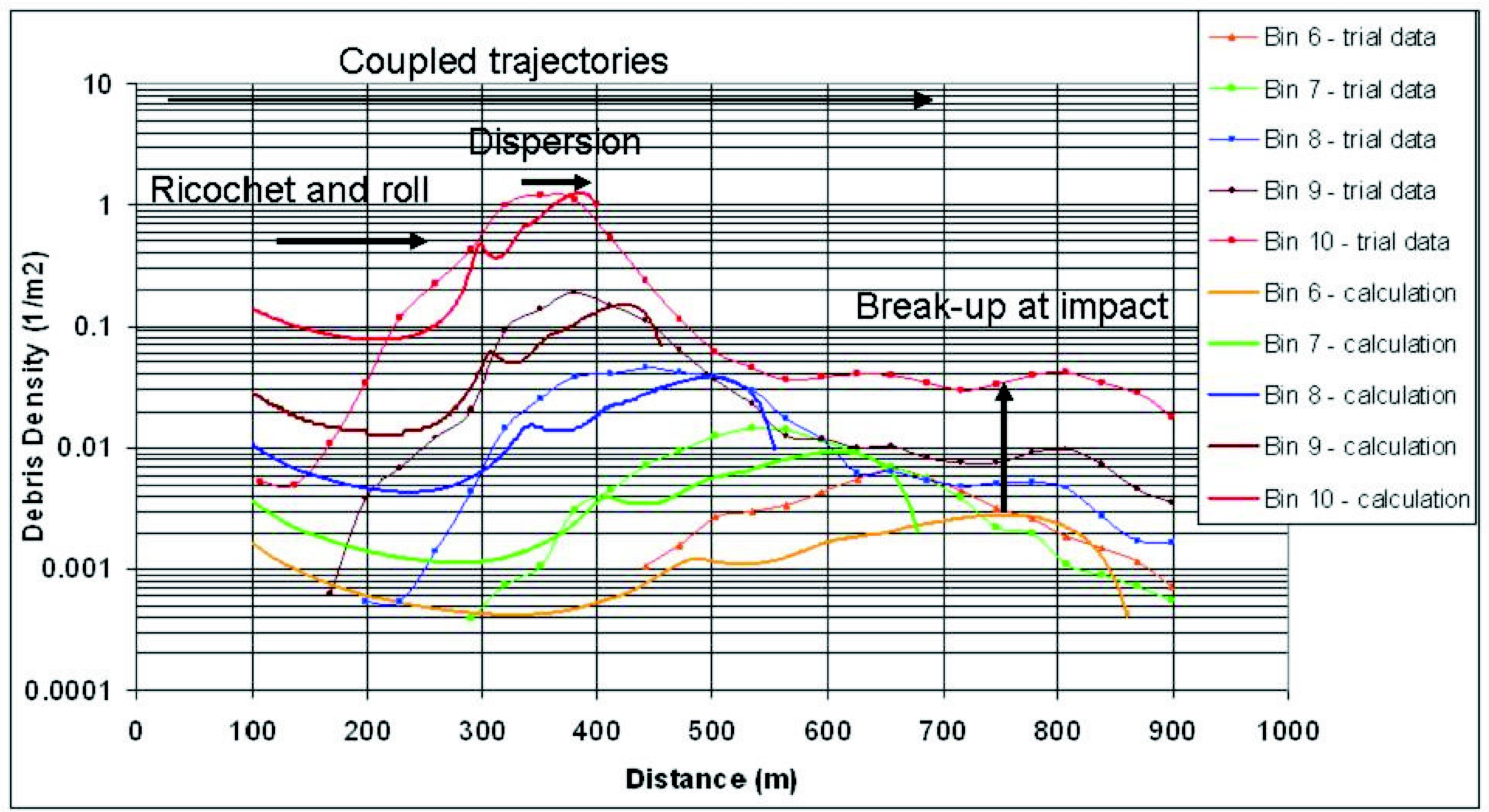 Fig. 4: Debris density calculated with the universal throw model together with experimental result. Sci pan 3 trial ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=vanderVoortMM:2006 | vanderVoortMM:2006)]] In Fig. 4 an application to the Sci Pan 3 trial is shown together with experimental results (vanderVoortMM:2006). Compared to hydrogen detonations, this trial is situated at the other end of the loading density regime (> 100 kg/m3), but illustrates the validity of the model in general. The calculations are in reasonable agreement with the experimental data. Differences can be recognized and understood as the model does not take into account:
In reality, these phenomena play a role, but are, on the other hand, not always important in the field of risk assessment. Solutions as suggested in (BaumMR:1999); (BakerWE:1983); (UFIP:2002) are widely applied and easy-to-handle models. The software PROJEX using a method developed by INERIS may also be used and seems to give better results (INERIS:2004). 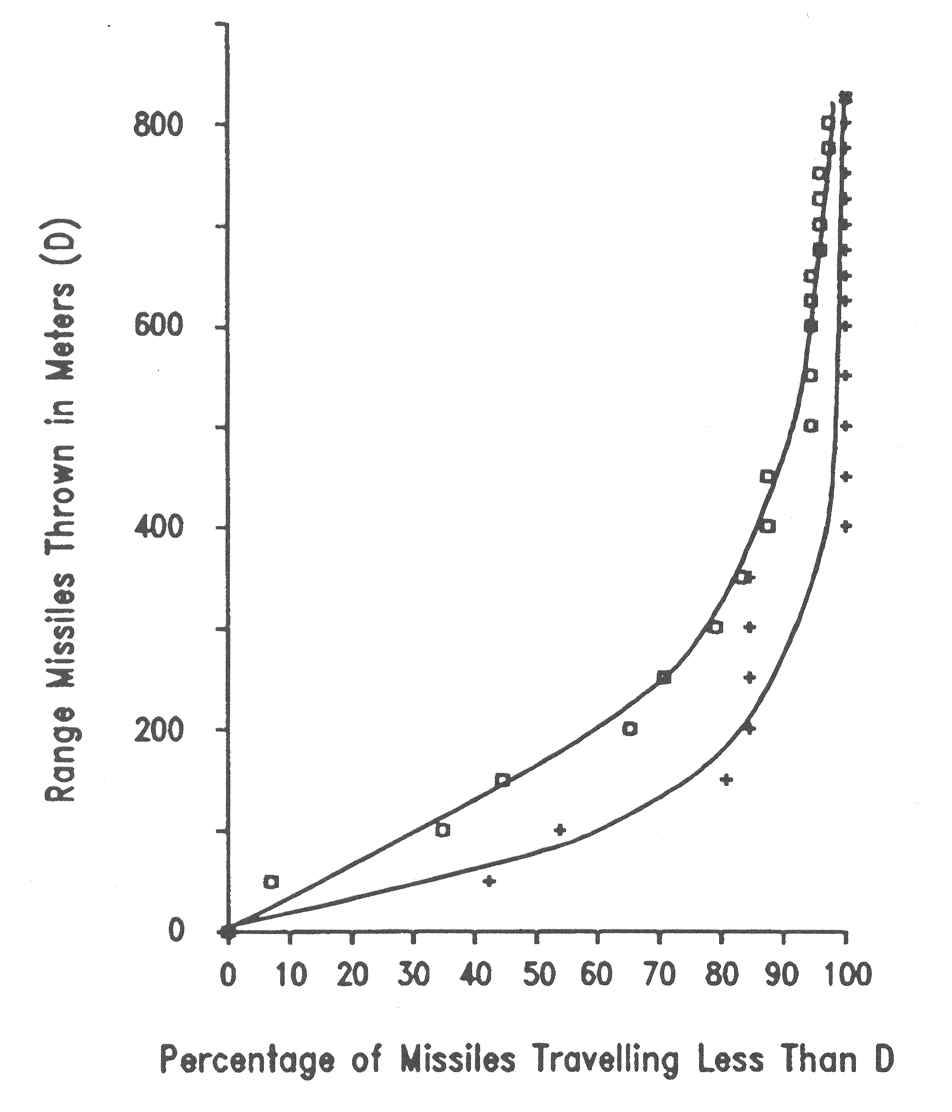 Fig. 3: Projectiles traveling after catastrophic pressure vessel failure +: experimental data; □: case studies ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=LeslieIRM:1991 | LeslieIRM:1991)]] Experimental data for the projectile hazards from bursting pressure vessels is displayed in Fig. 3-12. Data available are either from actual plant accidents on a large scale or from small-scale testing. The analysis shows among other findings that 80 % of all vessel ruptures resulting from fires lead to missiles, that non-fire ruptures have an increased number of fragments, that spherical vessels produce more fragments than cylindrical vessels, or that the end tubs of vessels travel further than other types of fragments. There is also the observed tendency of missiles to export fire (LeslieIRM:1991). Invalid BibTex Entry! Interaction of Blast Wave with Structure and Structural ResponseThe effects from an explosion, which have an impact on structures, are pressure changes (blast wave) and air movement (“explosion wind”) as well as thermal radiation and flying missiles. Only a third of the chemical explosion energy is involved in the generation of the detonation blast wave; the other two thirds are released much slower during the subsequent mixing and burning of the detonation products with the air (FEMA426:2003). In general, structural responses are highly dynamic, highly inelastic, and highly interactive. The mechanical effect of a blast wave is determined by the overpressure and the duration of the positive phase. 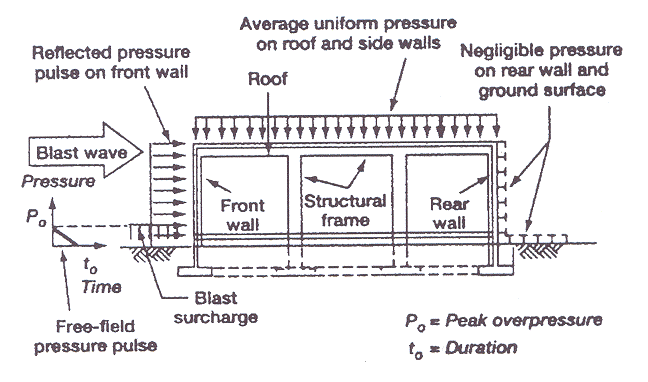 Fig. 1: Simplified blast loading diagram on a rectangular building ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BenteftifaCA:1995 | BenteftifaCA:1995)]] The blast parameters are dependent on the distance between structure and blast center. At close distances, the target is exposed to a high-intensity pressure load over a localized region; at greater distances, the load is reduced, but covers a larger surface area. The diagram in Fig. 1 describes the pressure load on a rectangular structure. The dynamic interaction of a blast wave with the structure depends on the pressure-time history, i.e., rise time and duration of positive phase and peak pressure or the impulse (which is the time integral of the pressure). Two phases are distinguished: 1. The initial “diffraction loading” 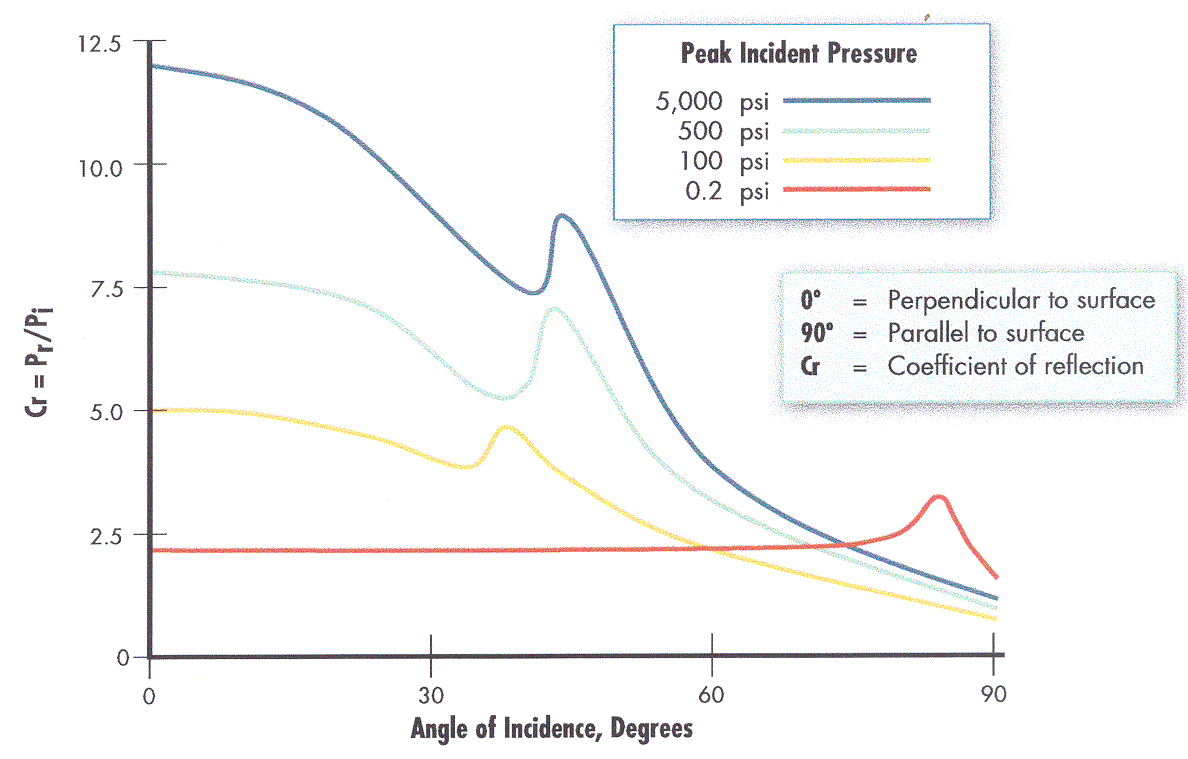 Fig. 2: Reflected pressure coefficient as a function of the incidence angle (100 psi = 2.26 MPa) ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=FEMA426:2003 | FEMA426:2003) ]] Diffraction loading is given by forces resulting from direct and reflected pressures during the initial phase. Reflection of the pressure wave at the front side amplifies the incident peak pressure with a normally reflected wave to represent an upper limit. Also density and temperature of the reflected wave are increased compared to the incident wave. The flow around the obstacle determines the further pressure development at the front and at the back side. The net horizontal loading is that on the front minus that on the back face. The reflection coefficient, i.e., the ratio between reflected and incident overpressure, is dependent on the blast wave type (pressure or shock wave), its intensity, and on the incident angle. For a pressure wave, this coefficient can have a value up to about 3 depending on the incident angle (the more usual case will have an oblique incidence). For a shock wave, it can be in the range of 2 to 8 and even higher for explosives (Fig. 2). Dynamic loads of fast transient pressures are imposed, if the combustion energy is inhomogeneously distributed, and are specific to the structure geometry. 2. The “drag loading” After the diffraction phase is completed, the structure is subjected to a “stagnation pressure”. The distance of the incident wave when interacting with the structure, causes major pressure differences developing from the edges of the structure. Resulting from this rarefaction wave, pressures decrease. During this so-called drag phase, strong transient winds (explosion wind) with flow velocities of several 100 m/s are effective. Drag forces will particularly have an impact on smaller structures such as pipe work. Load duration during vapor cloud explosions may be long enough to be comparable with the time required for the dynamic response time of the structure. In case of large structures, the rarefaction from the edges is insignificant. Confined Areas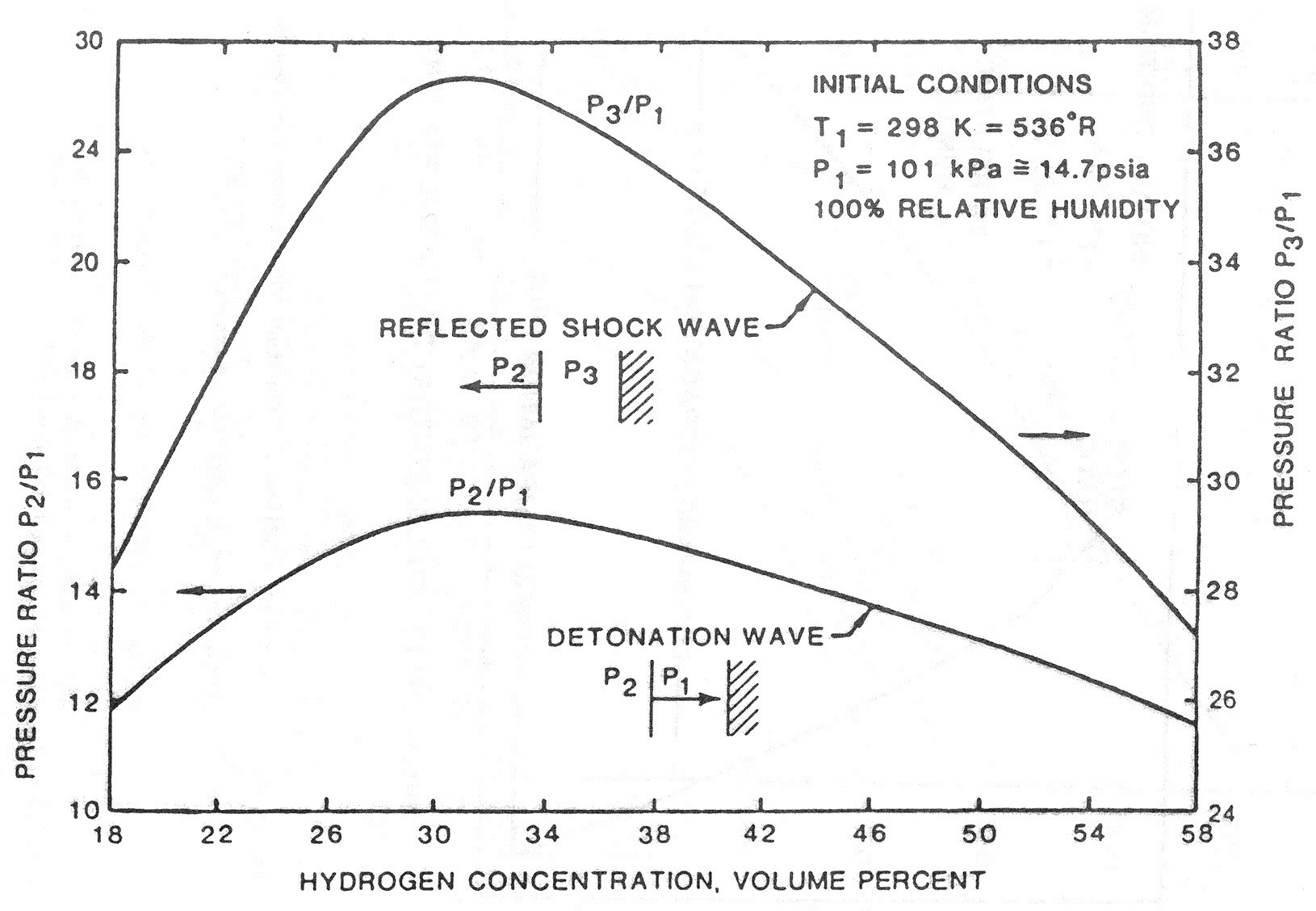 Fig. 3: Theoretical detonation pressure and normally reflected detonation pressure for hydrogen-air mixtures (IAEA 1990) 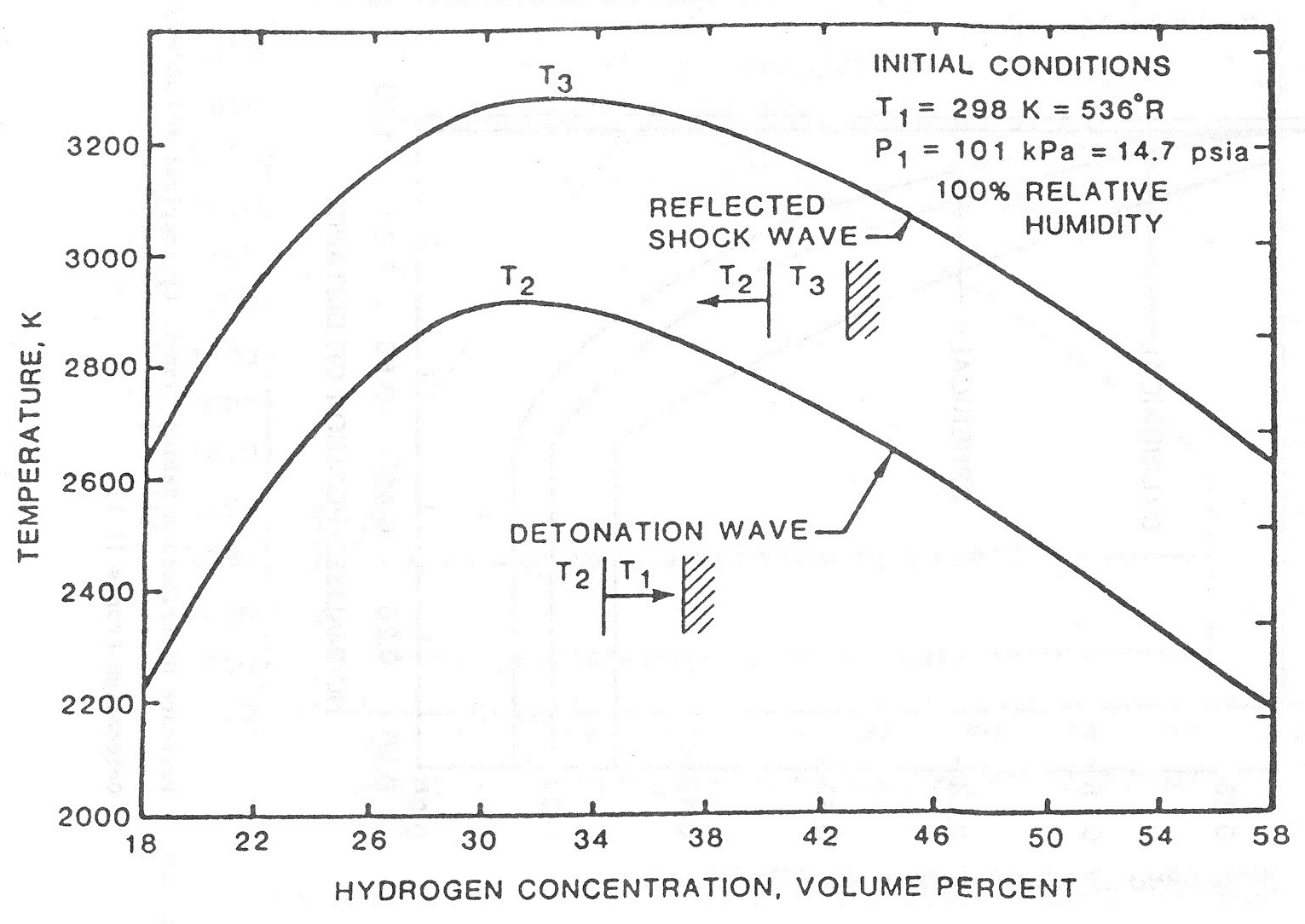 Fig. 4: Theoretical detonation temperature and normally reflected detonation temperature for hydrogen-air mixtures ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=IAEA:1990 | IAEA:1990)]] In a confined or partially obstructed area, an explosion will create a structure loading, where two phases can be distinguished, the reflected blast loading followed by the gas loading phase. When the pressure wave hits the (rigid) wall, gases are brought to a rest and the wave is reflected. At normal incidence, the reflected shock wave further compresses the burnt gases increasing the pressure by about a factor of 2.3. The mixture of reflected pressure waves and deflected air flows are the result of reverberation of the initial high-pressure, short-duration reflected wave with the amplitude decaying with each reflection until eventually pressure levels out at gas pressure loading. The latter phase lasts longer, the less venting is available. The more complex the structure, the more difficult is the prediction of the critical conditions for mechanical failure for a given load history. For a vented volume or a volume with weak surfaces, venting formula (NFPA68:2002), (prEN14994:2004) may be a tool in order to predict the pressure applied. In case of a detonation, the loading may be divided in two parts (USACE:1990), a shock pressure and a constant load. Invalid BibTex Entry! Forces acting on a structure will lead to a deformation to an extend which depends on the material properties and structure composition. For a static or quasi-static load, i.e., a constant or slowly changing load like from a simple deflagration, it will be in equilibrium with the internal forces resulting in a deformation of the structure. For a dynamic load, i.e., a fast load transient, however, a “dynamic” contribution from inertia forces will add to the equilibrium, which can show positive or negative acceleration, i.e., mass and stiffness of the structure will play a major role. The load from a gas explosion is considered a dynamic load due to its short overpressure duration, which is typically in the range of 100-200 ms. Detonations tend to excite the high natural frequencies of a building, whereas deflagrations are more effective for the lower frequencies. It appears to be technically more difficult to design a building against both explosion modes rather than only one. Methods used in order to determine structural response and resistance belong to three main categories:
Empirical Methodsa) Methods Based on Pressure Peak Values 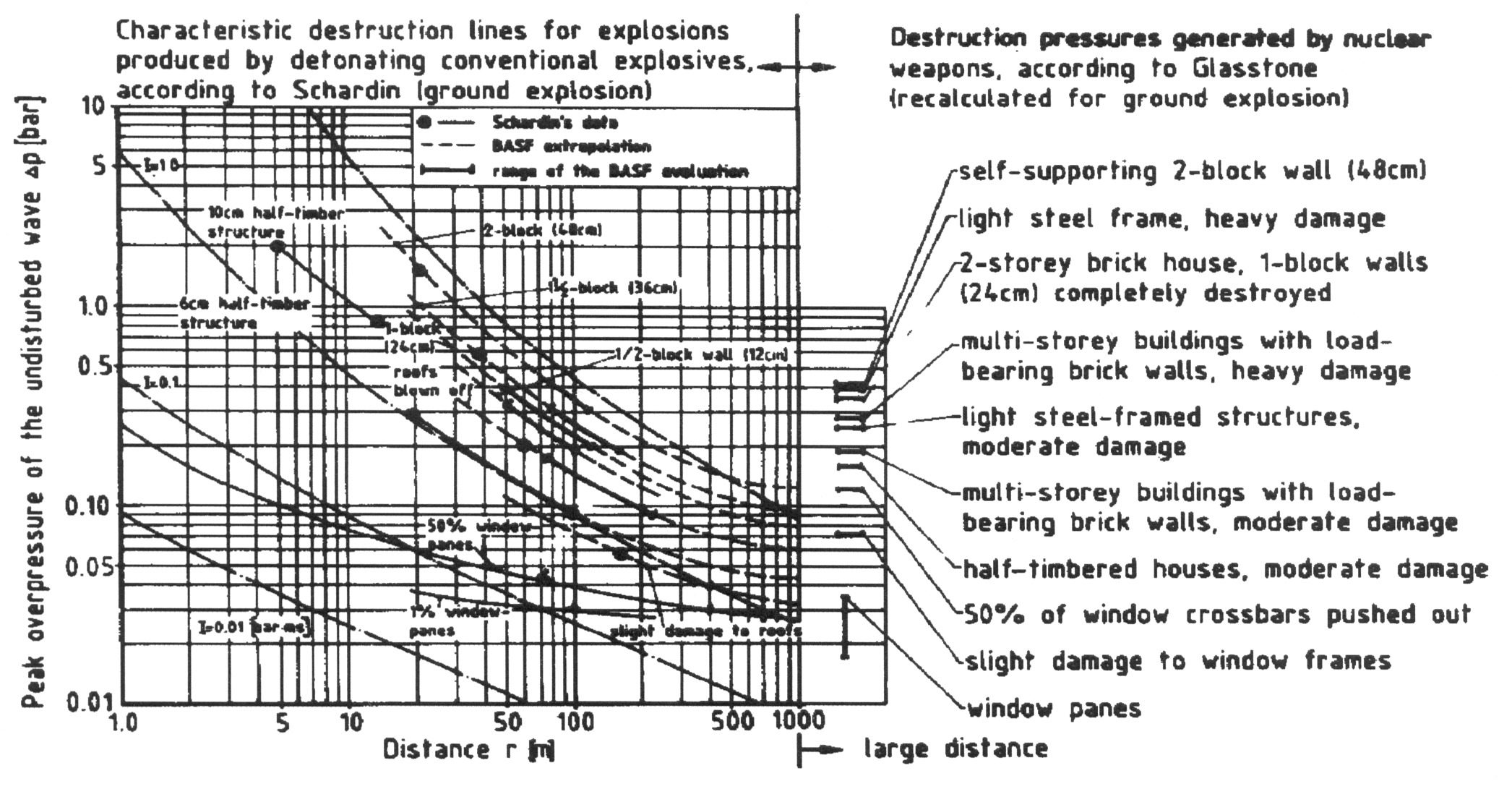 Fig. 1: Schardin destruction curves for detonation waves ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=GiesbrechtH:1988 | GiesbrechtH:1988)]] An empirical and very global approach of determining the strength of structures is to relate overpressures to the degree of observed damage. This very useful and easy handling method is widely used. The relationship between pressure and damage, which is derived from TNT explosions, cannot satisfactorily be transferred to vapor cloud explosions. The pressure decay from a TNT explosion is much faster than from a vapor cloud explosion. The high impulse and the suction effect due to the below-atmospheric pressure phase will certainly result in a different damage pattern. Thus damage criteria such as those derived by Schardin (see Fig. 1) from TNT explosions are not directly applicable (GiesbrechtH:1988). Many pressure criteria were defined in the past related to various structures and specific components, however, varying over a large uncertainty range. A rough classification is given in Table 1. Table 1: Damage classification (CPR16E:2005:GreenBook)
A pressure peak for domino effect really useful for risk assessment may also be defined at a value of 20 kPa (MEDD:2004). b) Methods based on P-I diagrams  Fig. 2: Transient behavior of impulse ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=FEMA426:2003 | FEMA426:2003)]] Another global approach may couple pressure peak with impulse. The impulse, i.e., the pressure – negative and positive – integrated over time, is a measure for the explosion energy (Fig. 2), which also varies in time and space over the exposed structure surface. Damage to the structure resulting from a blast wave may be subdivided into direct effects and what is named “progressive collapse”, a kind of secondary failure following the change of the load pattern on a structure due to the direct effects. Features of a P-I diagram are the asymptotes in P and I direction and the monotonic relation between P and I, which suggests a subdivision into three regimes: impulse-controlled, peak load-controlled, and an intermediate dynamic stage (LiQM:2002). P-I diagrams are being widely used in damage assessments not only for structural damage, but also for predicting blast-induced human injuries. They are providing useful information on the vulnerability of targets. 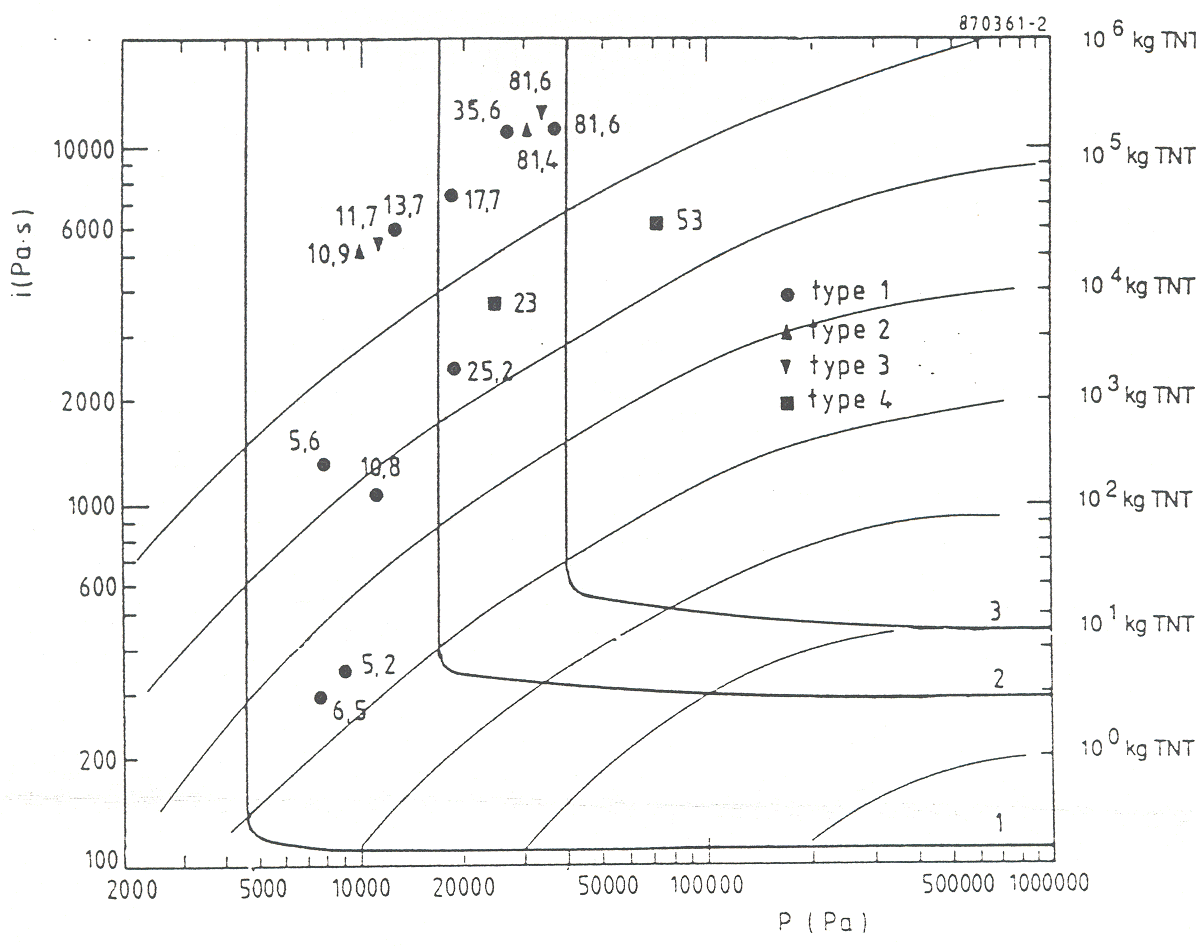 Fig. 3: Pressure-impulse diagram with experimental damage values for different types of houses ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=MercxWPM:1991 | MercxWPM:1991)]] Damage levels can also be visualized in pressure-impulse diagrams, where different regions can be defined by iso-lines. An example is given in Fig. 3 showing the experimental results for the observed damage in per cent, after different types of houses were exposed to a certain explosion (pressure/impulse) load (CPR16E:2005:GreenBook). Important for the damage effect of a short-term load (= shock wave) is only the impulse, whereas it is the maximum overpressure for that of the longer-term load (= pressure wave). The solid lines in the figure indicate the lower boundaries for light damages, for severe damages, and for collapsing structures of the houses investigated. The estimation of the level of damage is usually done taking either fixed-limits methods or the PROBIT method. In a fixed-limits method, the hazard level is compared to fixed limits like IDLH (Immediately Dangerous to Life or Health) values or pressure thresholds, as given in the literature. It is a simple method, but may lead to wrong conclusions in transient hazards. In such cases, the PROBIT method is the more appropriate one. First a hazard load, L, is estimated, which could be the overpressure in an explosion or the integrated thermal flux at a certain location. Then the PROBIT or probability unit, y, is given by y = k1 + k2*ln L, which can be related to a certain probability of death, injury, or damage. k1 and k2 are empirical parameters, which are specific to, e.g., toxic chemicals or fire and explosion effects and can taken also from the literature (CSCHE:2004). For the assessment of the probability to obtain a certain level of damage, so-called probit functions have been introduced and suitable damage criteria have been defined (CPR16E:2005:GreenBook). Computer simulation techniques have been developed by SRI International, USA, for analyzing hydrogen explosions and the subsequent response of structures and humans. The thermodynamic code TIGER is used to calculate explosion pressures and expansion characteristics, which are input to the DYNA3D model to determine the impact on structures. A simplification of the blast load damage analysis has led to the development of the pressure-impulse (PI) methodology which is based on the observation that for a broad range of structures, the final damage state depends on peak pressure (P) and total impulse intensity (I) only. This methodology allows for a quick and easy evaluation of accident scenarios by employing a continuously growing library of pressure-impulse load and damage curves that are based on either experimental data or computer simulations (Sanai 1996). Analytical MethodsA structure can be schematically represented by a system of masses coupled with springs or dampers. For the static case, if linear-elastic or non-linear-elastic forces are acting, displacements of the masses become zero again, when the load disappears. In case of plastic or elasto-plastic behavior, displacement is zero or very small, until the maximum load is reached. Under a static load, the structure will then fail; under dynamic load, it may retain a residual displacement. In general, structures must be designed to react elastically under typical loads like wind. Plastic displacement must be limited to abnormal load conditions. The maximum displacement depends on load duration, tD, and the natural frequency of the structure, T. For low tD/T ratios, the displacement is smaller than for static loads. For large tD/T ratios, the displacement can be larger than under static load conditions. Other important parameters are the static strength and the ductility. Load schemes are distinguished between a step function for a long-duration pressure wave and an impulse load for a short-impact shock wave. Detonations tend to excite the high natural frequencies of a building, whereas deflagrations are more effective for the lower frequencies. It appears to be technically more difficult to design a building against both explosion modes rather than only one. However for hydrogen explosions experience proves that detonations or strong deflagrations must be preferred. Several analytical procedures may be distinguished. They have to be coupled with structural engineering calculations. Still these methods are likely to lead to very conservative structural designs, and are rather suitable for hand calculations. A comparison between detonations of explosives and blast waves resulting from nuclear weapon explosions, characterized by quasi-static pressure due to a longer impulse time shows that, assuming the same damage, the detonation pressure or the pressure resistance of an object is much higher than the resistance against a blast wave from nuclear tests (PfortnerH:1975). The pressure resistance behavior of a building under detonative dynamic and quasi-static loading derived from numerous detonative explosion studies can be summarized in an empirical equation for the quasi-static reference overpressure of the building pst: pst = 0.15 * pr2/3, where pr is the perpendicularly reflected overpressure or the pressure resistance of the building subjected to a detonation. If the TNT equivalent, as derived from the damage of some of the severe accidents, is interpreted as the incident pressure wave in the order of 70 kPa, resulting from a deflagration, the respective quasi-static pressure would be with pst = 22 kPa much smaller. a) Dynamic Load Factor DLF The analytical procedure is usually simplified by introducing a so-called dynamic load factor (DLF), which is defined as the ratio of maximum dynamic displacement over static displacement. It transforms a dynamic peak load into a static load with the same effect on the structure. The DLF is dependent on the dynamic load time and the natural frequencies of the structure. For long explosion times and in case of an idealized triangle-shaped shock wave load, the DLF approaches its boundary limit of 2 (MEDD:1994). b) Single Degree-of-Freedom Model SDOF In a simple method, a static working load is assumed to simulate the effects of blast loads onto structures. This conservative approach, however, cannot predict structure performance and seems to be not optimal for transient blast loads. An improvement of modeling is given with the quasi-static methods which specify a triangular pressure pulse and determine the dynamic structural capacity as a function of the material strengths of the structure. The structural response can be found by using the charts. Single degree-of-freedom (SDOF) models analyze critical components in terms of their structural resistance and predict the response of the structure which then determines the damage level (USACE:1990)(USACE 1990). Numerical MethodsMore information is obtained from multi-degree-of-freedom (MDOF) models, sophisticated CFD models with the possibility to consider flame propagation and pressure profiles also from local explosions. Dynamic finite-element analyses with tools such as ADINA, LS-DYNA, AUTODYN, ABAQUS Explicit may provide the best judgement on whether or not a structure is able to withstand a blast wave. However, one must be very careful when using software which is still under development and which is still not fully validated to industrial applications. Numerical methods are also usually very sensitive to parameters and calculation grid changes. Invalid BibTex Entry! Heat RadiationThere exists an extensive published literature on flame radiation from hydrocarbon flames and pool fires, see, for example, (DeRisJ:1979); (TienCL:1982); (MudanKS:1984); (FaethGM:1985); (ViskantaR:1987). However, there is a limited number of studies on hydrogen flame radiation, particularly on large scale. Thermal radiation is a primary mode of heat transfer. Radiation is the dominant mechanism of heat transfer in large fires involving hydrocarbons, producing intermediate unstable radicals (e.g., O, H, OH, N, etc.) and stable non-luminous gaseous combustion products (CO2, CO, H2O, NOX, etc.) and soot particulates. The contribution to the radiative transfer in flames can be regarded as due to luminous and non-luminous radiation. Non-luminous flame radiation originates from transitions in the molecular energy levels due to the absorption or emission of photons. Discrete absorption-emission lines of radiation are produced in the infrared spectrum as a result of transitions between quantised electronic states for monatomic gases. Energy released by the gaseous combustion products results from the transitions between the vibrational and rotational energy levels of the molecules of gas species, particularly CO2, H2O, CO, etc., producing non-luminous radiation concentrated in spectral lines. These gases do not scatter radiation significantly but they are strong selective absorbers and emitters of radiant energy. In practical engineering systems, where pressure and geometric scales are large, pressure broadening of spectral lines cause them to overlap with each other, The resulting radiation is thus concentrated in gaseous absorption bands in infrared spectrum produced by various types of transitions between the molecular energy states, particularly the vibrational-rotational states. In luminous flames a continuum radiation in the visible and infrared is also emitted by the unburnt carbon particulates called soot that contribute greatly to the luminosity of the flames. The actual quantity and distribution of combustion products and/or soot produced in fires depend on the type and configuration of fuel and local supply of oxygen. In contrast to hydrocarbon fuels, the hydrogen burns more cleanly in air, producing non-luminous, almost invisible, pale blue flame due to spectral water vapour bands. In order to understand thermal radiation hazards from hydrogen flames, it is crucial to understand the relative assessment of the physical properties and combustion characteristics of hydrogen and hydrocarbon flames. Table 3-2 provides comparison of the physical properties of hydrogen with hydrocarbon methane. Table: Physical properties of hydrogen and methane
Hydrogen has a much wider range of flammability in air (4 % to 75 % by volume) than methane (5 % to 17 % by volume), propane, or gasoline, and the minimum ignition energy (for a stoichiometric mixture) is about an order of magnitude lower (1/16th that of methane). In many accidental situations the lower flammable limit (LFL) is more important. The LFL for hydrogen is similar to that of methane, about twice that of propane, and four times that of gasoline. In addition, the minimum ignition energy for hydrogen at the LFL is also similar to that of methane. Hydrogen-air mixture can burn either as a jet flame at a fixed point, with combustion taking place along the edges of the jet where it mixes with sufficient air. In a stationary mixture in the open with no confinement a flammable hydrogen mixture will undergo slow deflagration. Deflagration refers to a flame that relies on heat- and mass-transfer mechanisms to combust and move into areas of unburned fuel. If the flame speed is accelerated, perhaps due to extreme initial turbulence or turbulence induced by obstacles or confinement, the result is an explosion. In the extreme case the flame speed becomes supersonic and results in detonation. Once initiated, detonation is self-sustaining (no further turbulence or confinement is required) as long as the combusting mixture is within the detonable range. The heat of combustion of hydrogen per unit weight is higher than any other material, but hydrogen has a relatively low heat of combustion per unit volume. Thus the combustion of a given volume of hydrogen will release less energy than the same volume of either natural gas or gasoline. Invalid BibTex Entry! In contrast to other hydrocarbon fuels, a hydrogen flame radiates significantly less infrared (IR) radiation (heat) and virtually no visible radiation (light). As a result, hydrogen burns with a pale blue, almost invisible flame that is almost visually imperceptible in artificial light or daylight. However, in contrast to hydrocarbon flames, hydrogen flame also emits some limited amount of radiation in the ultraviolet (UV) region around 180 to 300 nm, which is exploited by UV detectors to detect hydrogen flame. Most UV detectors are made immune to solar sensitivity by using a sensing device only sensitive to the UV radiation below the 360-nm range. The lower radiation from a hydrogen flame makes the flame itself hotter than a hydrocarbon flame, and objects engulfed by a hydrogen flame tend to heat faster. However, the lower radiation of heat from the flame means that less heat is radiated to objects or people outside the flame. The consequence of the almost invisible hydrogen flame is that the human physical perception of the heat from a hydrogen fire does not occur until direct contact with the combustion gases. This problem is often resolved by throwing a dry fire extinguisher or dust into the air that will cause the flame to emit visible radiation. 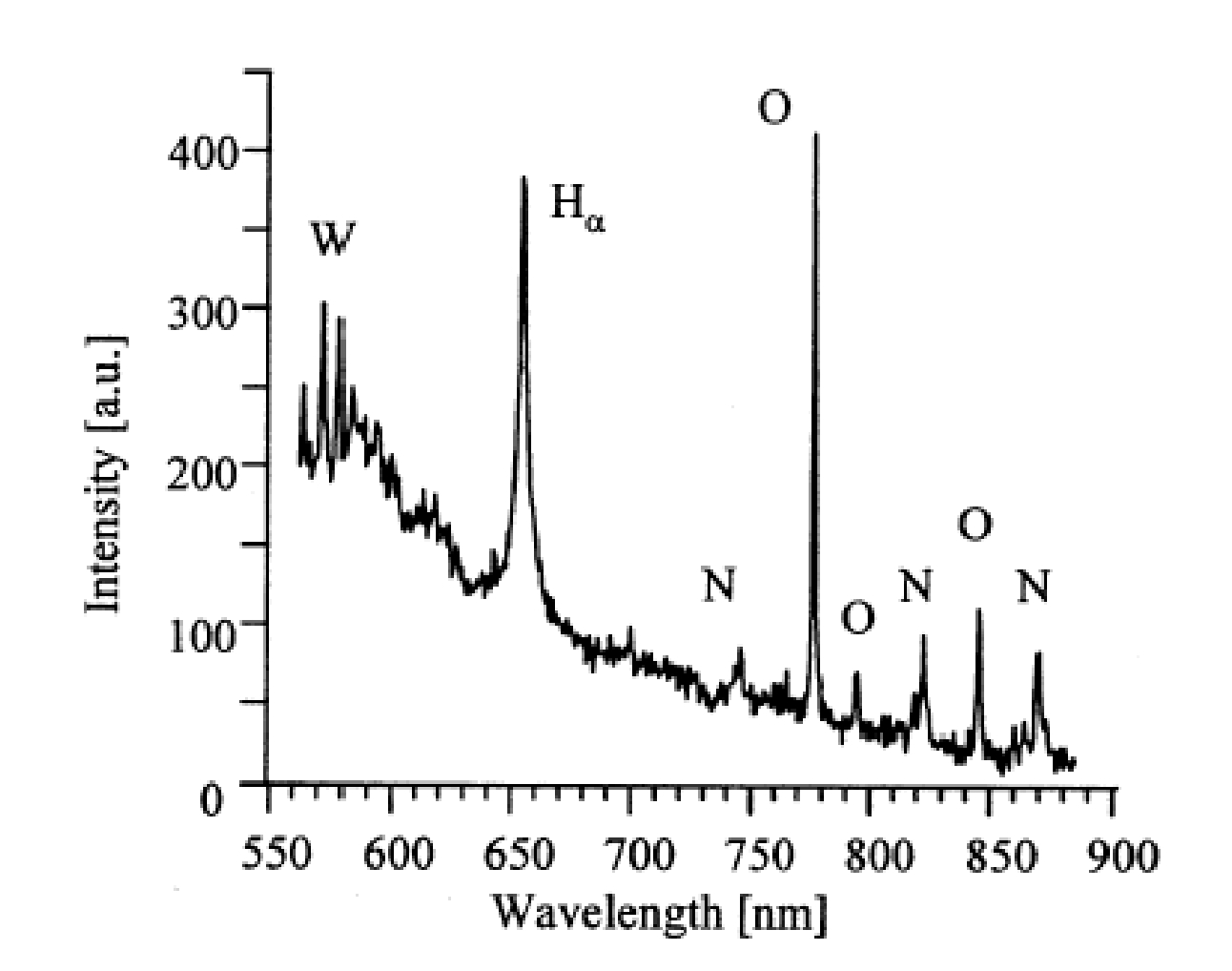 A typical spectrum of laser induced plasma spectroscopy (LIPS) in a hydrogen-air flame for wavelength range of 550-900 nm ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=ItohS:2001 | ItohS:2001)]] The combustion chemistry of hydrogen flame gives rise to H, O and N atoms, and OH radicals, which emit specific peaks at specific wave lengths. The typical emission spectrum of the laser-induced plasma spectroscopy (LIPS) formed in hydrogen-air flame in the infrared region is shown in the figure, and their wavelengths are listed in the table. LIPS is a promising method that enables spatially resolved elemental analysis of various chemical species based on their atomic emissions. The spectrometer was set to be centred at a wavelength of 720 nm so that atomic emissions of hydrogen H, nitrogen N, oxygen O, and tungsten W could be observed simultaneously. The continuum spectrum is also observed with the emission lines, which is mainly due to the recombination of ions with free electrons. Table: Wavelength of each emission line (ItohS:2001)
More recently, (ChoudhuriAR:2004) have used laser-induced fluorescence (LIFS) technique for measurements of H atom near 656 nm (2s → 3p) O atom near 845 nm (3s 3S), and OH hydroxyl radical in the UV region near 315 nm. The OH radical is one of the important intermediates in the combustion reaction mechanism, which is a reliable indicator of the flame zone, flow structure and flame temperature near stoichiometry. Here, the flame temperature was determined by measuring the rotational energy distribution of the OH radical at the excitation of (1,0) band of (A2 Σ ← X2 Π) system. Please note that it is not possible to avoid interference of the photolytic production of O atom at the wavelength of 845 nm with the adjacent NO excitation band (1,1) of (A2 Δ ← X2 Π) system. Here the symbols s, p, d stand for the atomic orbitals and Σ, Π, Δ stand for the molecular orbitals. Maximum statistical uncertainties in measurements were estimated to be 20-30 K in the temperature range. Invalid BibTex Entry! The hydrogen-air flame emit infrared (heat) radiation mainly due to water vapour bands in the 1-6 μm wavelength region. The contribution of atoms and radicals to heat radiation in hydrogen flame is negligible. However, as mentioned earlier, OH radical effects the maximum temperature of the flame. 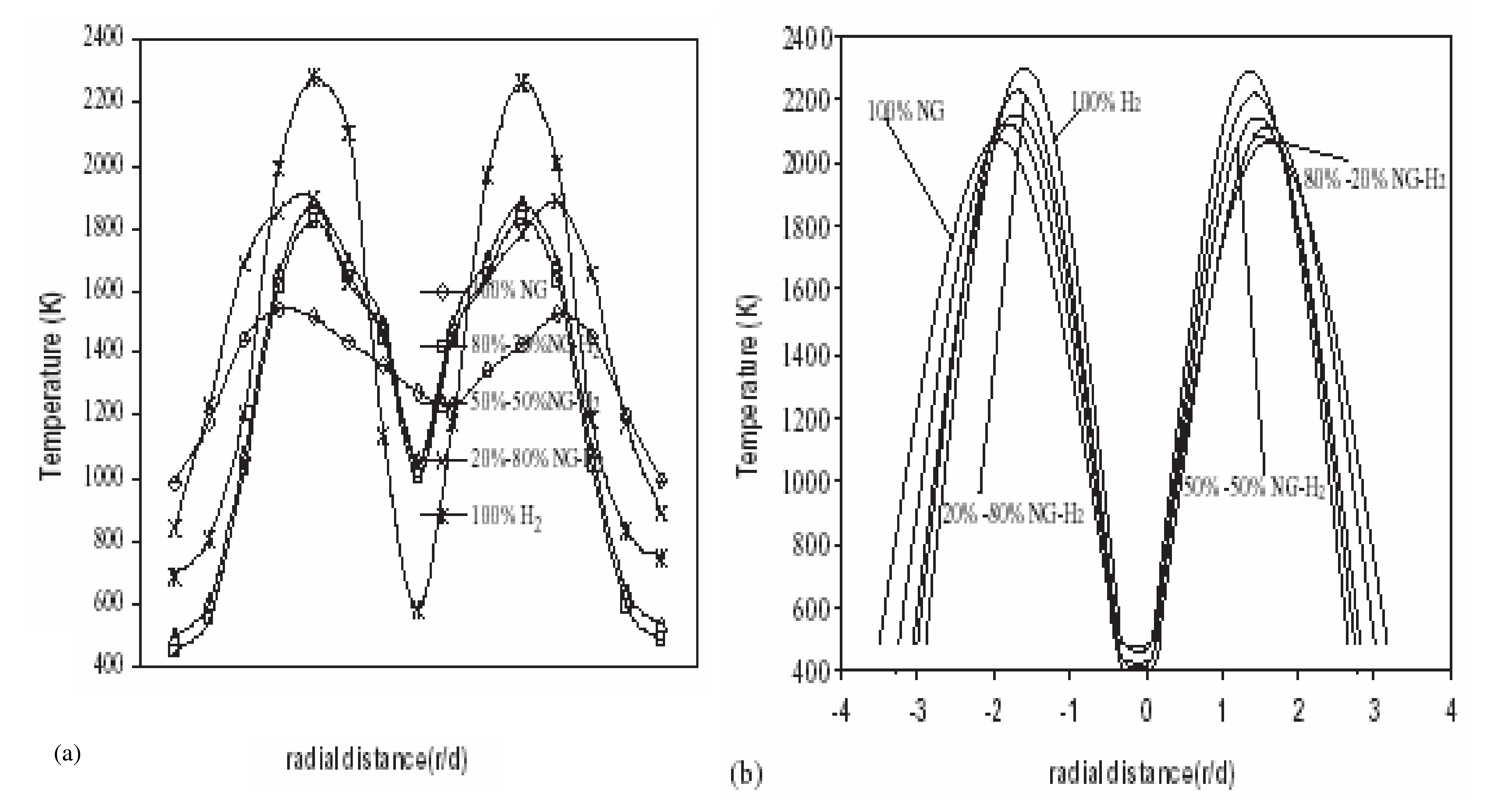 Radial temperature distribution at the near-burner region (a) spectrally derived from OH measurements (b) computed using detailed chemical kinetics ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=ChoudhuriAR:2004 | ChoudhuriAR:2004)]] Figure 1 shows the comparison of the predicted and measured radial temperature distribution of H2-air flame for different degrees of dilution by natural gas, the dilution ranging between 0 and 100 %. The measured values shown in Fig. 1(a) have been derived from OH fluorescence signals, and the predicted values shown in Fig. 1(b) have been computed using detailed chemical kinetics. It can be seen from the figure that the peak temperature of the 100 % hydrogen-air flame is 2320 K and that of the 100 % natural gas-air flame is 1600 K. The lower peak temperature of the natural gas flame is attributed to the higher heat losses both in the form of banded non-luminous radiation from CO2 and continuous luminous radiation from solid soot particulates, which are absent in the H2-air flame. Both flames have heat losses from banded non-luminous radiation from H2O. The computed stoichiometric temperature contours using the detailed chemical kinetics show a similar trend for the different mixture conditions. Compared to experimental results, predicted temperatures are higher and steeper in shape for all mixture conditions. Liu et al. (LiuLH:2004) have considered 6.3 μm, 2.7 μm, 1.87 μm, and 1.38 μm infrared bands of water vapor to calculate frequency distributions of radiative source terms. Due to different band intensity parameters and temperature for each band, the symmetrization of frequency distributions in each band is different. The symmetrization of frequency distributions for the radiative source term at 6.3 μm and 2.7 μm bands is better than at 1.87 μm and 1.38 μm bands. Invalid BibTex Entry! Flame radiation intensities or fluxes are often computed from mean properties (e.g., mean emissivity, mean flame temperature). However, Cox (CoxG:1977) has shown that neglecting turbulent fluctuations could cause significant error in flame radiation intensities, which is due to non-linear nature of radiation properties. Assuming a gray gas, the mean radiation intensity can be represented as:
where σ is the Stefan Boltzmann constant, φ is the geometrical view factor, &eps; is the gray gas emissivity of flame, T is the flame temperature, and I is the flame intensity. While this result suggests a strong effect of turbulence on radiation properties, the gray gas approximation is not very appropriate for turbulent flames. However, Faeth et al (FaethGM:1985) have shown that the use of mean properties, in conjunction with existing narrow band models, provide an adequate framework for estimating flame radiation in both non-luminous and luminous flames. The figure shows the comparison of the predicted spectral radiation intensities by the mean and stochastic property methods with measurements, in the 1-6 μm wavelength range, for a turbulent hydrogen/air flame. The stochastic method is based on the assumption that the turbulent flow field consists of many eddies and that the properties of each eddy are uniform and statistically independent of one another. The figure shows that for hydrogen/air flames, effects of turbulent fluctuations are large, with as much as 2:1 difference between mean and stochastic property predictions. Faeth et al (1985) have argued that this is because radiation properties of hydrogen/air diffusion flames vary rapidly near the stoichiometric condition. Invalid BibTex Entry! The theory of thermal radiation is very complex and an exact solution, even for reasonably simple situations, is generally impossible. The combustion products and soot, acting as participating media, add further complexity to the situation. Therefore, a wide range of calculation methods and mathematical models with varying levels of complexity and accuracy have been developed. A number of radiation solution methods exist for solving the equation governing the transfer of thermal radiation (SiegelR:1993). The methods differ in complexity and accuracy of the calculation of view factors and economy of the solution algorithm. The most commonly used radiation solution methods and their key features are summarised below: Factor Zonal or View Calculation MethodThis popular method has been widely used by engineers to estimate the radiative transfer in the absence of detailed knowledge of participating media. The walls and interior of the enclosure are divided into zones of finite size. View factors are defined which are measures of the radiation exchange occurring between pairs of zones. This procedure results in n simultaneous equations for each of the n zones and leads to a system with a n2 x n2 matrix. This method is very accurate but its main drawback is that the view factor, for each geometry, must be worked in advance and for complex geometries the view factors are not available (Hottel and Cohen 1958). Statistical or Monte-Carlo MethodThe purely statistical methods, such as the Monte-Carlo method, usually yield radiation heat transfer predictions as accurate as the exact method. There is no single Monte-Carlo method because there are many different statistical approaches. The simplest Monte-Carlo method is based on simulating a finite number of photons (discretized energy bundles) histories through the use of a random number generator. For each photon, random numbers are generated and used to sample appropriate probability distributions for scattering angles and path lengths between collisions. As the number of photons initiated from each surface and/or volume element increases, this method is expected to converge to the exact solution of a problem. Thus, this statistical method is numerically precise provided the number of photons is large and the random number generator of the computer good enough. Furthermore, in contrast to the zonal method, the Monte-Carlo method does also not suffer from the calculation of view factors in advance because the view factors are automatically calculated as the randomly chosen energy release bundles are tracked through the enclosure containing the fire. However, since the directions of photons are obtained from a random number generator of the computer used, the method is always subjected to statistical errors and lack of guaranteed convergence but this would improve as the next generation of computers (with more powerful random number generators) become more readily available (HowellJR:1964). The Flux (or Multi-Flux) MethodThe radiation intensity is a function of the location, the direction of propagation of radiation and of wavelength. Usually the angular dependence of the intensity complicates the problem since all possible directions must be taken into account. It is, therefore desirable to separate the angular (directional) dependence of the radiation intensity from its spatial dependence to simplify the governing radiation transfer equation (RTE). If it is assumed that the intensity is uniform on given intervals of the solid angle, then the RTE can be significantly simplified as the integro-differential RTE would be reduced to a series of coupled linear differential equations in terms of average radiation intensities or fluxes. This procedure yields the flux methods. By changing the number of solid angles over which radiative intensity is assumed constant, one can obtain different flux methods, such as two-flux for one-dimensional geometry, four-flux for two-dimensional geometry or six-flux methods for three-dimensional geometry. The accuracy of flux-methods will increase by increasing the number of fluxes. The six-flux methods have been reasonably successful for fire spread and smoke movement inside compartments (KumarS:1989a); (KumarS:1991). They are not suitable for predicting flame spread over surfaces or flames projecting outside openings, where finer discretization of the solid angle than offered by the six-flux method would be necessary (GosmanAD:1972). The Discrete Ordinate MethodThe discrete-ordinate method (e.g., (ChandrasekharS:1950); (LockwoodFC:1978); (FivelandWA:1982)) was originally suggested in (ChandrasekharS:1950) for astrophysical problems. It is derived by applying discrete-ordinate approximation to the RTE through discretising the entire solid angle (Ω = 4π) using a finite number of ordinate directions and corresponding factors. A simpler version of the method is also called SN-approximation because it is obtained by dividing the spherical space into N equal solid angles. More accurate SN-approximations of the N discrete ordinates are obtained by using Gaussian or Lobatto quadratures and choosing N discrete values of the direction cosines ζn, ηn, μn such that they satisfy the identity ζn2 + ηn2 + μn2 =1.The SN-approximation has been used successfully for two-dimensional cylindrical and rectangular radiative transfer problems with combustion chamber applications, where reasonably accurate results were obtained in comparison to exact solutions (FivelandWA:1982)(FivelandWA:1984). However, the method suffers from the so-called “ray effects”, causing anomalies in the scalar flux distribution (LathropKD:1968)(LathropKD:1971). The ray effects are particularly more pronounced when there are localised radiation sources in the medium (e.g., flame in an enclosure) and radiation is less important in comparison to absorption. Clearly, as scattering increases and radiation field becomes more isotropic, they become less noticeable. However, with increasing scattering and/or optical thickness, the convergence rate may become slow (LewisEE:1984). The Discrete Transfer MethodThe discrete transfer method is a mixture of the Monte-Carlo, zone and flux methods (LockwoodFC:1981). Similar to the zone method, the enclosure is divided into cells and equation is analytically integrated along rays in each cell, but the method is much faster and the calculation of the view factors is an inherent feature of the procedure. The only drawback of the method is that to obtain ray-insensitive solution the method may require more rays than affordable on economy grounds for practical problems (CumberPS:2000). Invalid BibTex Entry! 1. IntroductionBurning hydrogen emits thermal radiation in UV, NIR and IR spectral range. Especially in the case of a large vapor cloud explosion, the risk of heat radiation is commonly underestimated due to the non-visible flame of hydrogen-air combustion based on to effects. In the case of a real explosion accident organic substances or inert dust might be entrained from outer sources to produce soot or heated solids to substantially increase the heat release by continuum radiation. Besides pressure waves, radiation is the main effect to influence the surroundings and contribute to fire and explosion transfer and propagation. The radiative emission of hazardous fires and gas explosions is strongly variable in time at short scales down to milliseconds. In addition, it includes fundamental information concerning the mechanisms and progress of burning. A fast scanning analysis of the spectral flame radiation must be fast enough to detect pre-reactions, transient phenomena, starting explosions, and enables the understanding of propagation mechanisms as well as quenching or extinguishing mechanisms. In contrast to pressure effects, time-resolved radiation of fires and explosions is not yet investigated to a sufficient extend, especially concerning spectral resolution. There are only some publications on time-resolved emission spectroscopy of gas explosions ((EisenreichN:1986), (KolarikP:1991), (EcklW:1995), (WeiserV:1999)). Equipment for time and spectrally resolved investigation and methods of data evaluation to obtain temperatures and species as well as radiative power are described in the following sections. 2. Calculation of NIR/IR Spectra using BAM-CodeA quantitative data analysis of infrared spectra measured from flames and plumes of pyrotechniques has to be based on band modeling. An appropriate code, BAM, was developed by ICT which calculates NIR/IR spectra and allows least squares fits to experimental ones with temperature and concentrations being the fitting parameters (WeiserV:2005a). The calculations use the data from the Handbook of Infrared Radiation from Combustion Gases ((LudwigCB:1973), (FerrisoCC:1965)) which cover the temperature range from 600 to 3000 K. The computer program BAM calculates NIR/IR spectra (1-10 μm)of inhomogeneous gas mixtures of H2O (with bands around 1.3, 1.8, 2.7 and 6.2 μm), CO2 (with bands around 2.7 and 4.3 μm), CO (4.65 μm), NO (5.3 μm) and HCl (3.5 μm) and can take into account emission of soot particles. Self absorption and pressure line broadening can be taken into account. The calculation of an emission or transmission spectrum along an optical path starts from the determination of the absorption coefficients resolved with respect to wavelength. The spectral bands of three-atomic molecules consist of thousands of single lines, e.g., for important flame constituents, HITRAN ((KneizysFX:1988), (RothmanLS:2003)) lists nearly 50,000 lines for H2O and 60,000 for CO2, and simplified models to quickly obtain line positions and strength are currently not available. Therefore tabulated data are used. The calculation of a spectrum of diatomic molecules is based on the anharmonic oscillator and corrections for vibration-rotation interaction to end up with averaged absorption coefficients and line densities derived from the approach described above for spectra in the UV/Vis spectral range (HerzbergG:1950) for band modeling. The molecules which emit in the UV/Vis and consisting of C, N, O and H are quite well documented and analyzed ((HerzbergG:1950), (PearseRWB:1963), (MavrodineanuR:1965)). Calculated band profiles allow the calculation of temperature, in case of time resolution also time profiles ((DiekeGH:1961), (CoxonJA:1980), (ChidseyIL:1980), (SchneiderH:1988), (EcklW:1992), (EcklW:1992a)). The band models enable an effective calculation of radiation transport in inhomogeneous media in order not to apply a transport equation for each single line ((WeiserV:2005a), (LudwigCB:1973), (FerrisoCC:1965)). Line shapes, half widths and positions of lines contribute to the models. At high temperatures, a Random Band Model has proven to be appropriate using a Doppler-Lorentzian line shape. For the separated bands of the various molecules, the individual lines were accumulated to a Single Line Group, and for the Curve of Growth, the Curti-Godson approximation was used. Benefits, shortcomings and possible errors of this model are discussed in the Handbook of Infrared Radiation from Combustion Gases (LudwigCB:1973).  Fig. 1: BAM simulation of emission spectra of homogeneous gas layers of 30 mol% water in air with an optical depth of 1 m at different temperatures Figure 1 shows a BAM simulation of emission spectra of homogeneous gas layers of 30 mol% water in air with an optical depth of 1 m at different temperatures. Hydrogen reacts with the oxygen in air to water, which is a well known strong emitter of bands in near and medium infrared spectral range. Co-combusting hydrocarbons additionally produce emission active products like CO2, CH, CO, and soot. Thermodynamic equilibrium calculations of hydrogen/air and hydrogen/hydrocarbon/air mixtures in stoichiometric compositions of air numbers between 0.5 and 4 executed with the ICT code (VolkF:1982) result in a typical temperature in the range of 2000 to 2800 K. In a real explosion which might entrain dust and organics, these bands are to be expected to combine with bands of, for example, CH, CO2, CO depending on the special constraints of the experiment or accident. The analysis of the spectra enables to derive the progress of reaction, reaction front, hot reaction products and their expansion and temperature profiles. Well defined experiments should be performed to verify the spectral characteristics predicted by the calculations. 3. Experimental TechniquesHydrogen as a homo-nuclear, diatomic molecule does not show any bands in the NIR/IR spectral range. But in case of combustion in air, the formed water has many well known bands in this range. Additionally, this reaction provides quite an amount of heat radiation, so emission spectra could be taken. In the UV range, diatomic radicals could be observed. Emission Spectroscopy in the UV/Vis-Range (OMA) In the UV/Vis-spectral range, diatomic molecules emit specific systems whose structure is partially resolved. Determination of rotational and vibrational temperatures of various diatomic molecules and transitions from UV/Vis emission spectra is based on the calculation of line intensities and profiles. For acquisition of emission spectra in the UV/Vis range, commercial diode array spectrometers are available (EcklW:1995). At the ICT, an ANDOR spectrograph (OMA) is used equipped with a CCO detector with 1024 elements. To get rotationally resolved spectra, a grating with 2400 lines/mm can be chosen (wavelength resolution 20 cm-1). Minimum time resolution of the system is 10 ms. A grating with 300 lines/mm can be used, if no rotational resolution was needed. Wavelength calibration is performed by standard lamps of Hg and Ne, and the intensity calibration by black body radiator or tungsten strip lamp. A typical spectrum of an OH band is shown in Fig. 2.
Emission Spectroscopy in the NIR-Range (AOTF) An AOTF spectrometer system enabling the acquisition of spectra in the NIR range 1000-2500 nm at rates of up to 1000 scans/s at a wavelength resolution of 2-3 nm is also available. The intensity calibration was carried out by recording reference spectra of a black body radiator. A spectra series of a hydrogen/air gas explosion is given in Fig. 3.
Emission Spectroscopy in the NIR-Range (HGS)  Fig. 4: BAM evaluation of stoichiometric hydrogen-air mixture. Increase of emissivity after 0.5 s depends on surface heating of the vessel walls The fast scanning hot gas sensor (HGS) based on a Zeiss MCS 511 NIR spectrometer (WeiserV:2005a) is a grating spectrometer with an InGaAs diode array as detector (spectral range 0.9 to 1.7 μm). The spectral resolution is about 15 nm at a scan rate of 300 spectra per second. The imaging optics consists of glas fibre optic with a narrow slit, which achieves a space resolution of about 1 mm. The quantitative calibration occurred by a commercial black body radiator. Temperature, concentration of water, and emissivity could be calculated by using the BAM code as it is described above (Fig. 4). Emission Spectroscopy in the IR-Range (Filter Wheel Spectrometer) Spectra in the IR range are recorded applying a rotating filter wheel spectrometer. The spectrometer consists of a fast rotating wheel with three interference filter segments. They continuously vary the transparency in the wavelength regions from 2.4 to 5.5 μm (InSb detector) and 5.5 to 14 μm (InSb/HgCdTe sandwich detector). The system was developed at ICT to investigate fast combustion processes. The intensity calibration was carried out by recording reference spectra of a black body radiator. IR spectra show the bands of reacting components and products more detailed. In case of hydrogen combustion, intense water band systems will emit. In case of co-combustion of organic materials, additional emission bands of CO and CO2 as well as a continuum radiation of soot and other particles occur and particularly increase the total thermal output drastically. Thermo Video Camera An IR camera of AGEMA (Thermovision 900) recorded images of the radiation in the NIR/IR spectral range. The detector is sensitive between 3 and 5 ~μm wavelength. A filter could limit the detection to the CO2 band at 4.25 μm only. The frame rate is 30 s-1. Invalid BibTex Entry! The radiative properties (absorption and scattering coefficients) of the combustion products and enclosure wall emittance are required for the modelling. In an enclosure fire, the gas radiative properties vary considerably from the comparatively transparent entrained air close to the floor to the highly emissive, luminous flames of fire source, and the optically dense ceiling smoke layer. Various models are available to predict the gas radiative properties. The participating media models (see, for example, (TienCL:1982)) currently available for characterizing the flaming and smouldering fires and the resulting combustion products differ in their generality, sophistication, accuracy and computational cost. They are assessed in terms of their ability to predict radiative heat transfer from one-dimensional, idealised representations of the internal structure of buoyant and jet fires. Exact results can be obtained by line-by-line calculations of spectral absorption-emission lines of molecular gases. However, such calculations are useful in the study of radiative transfer in the atmosphere but are not practical for most engineering applications, and are therefore not discussed here. Narrow-band and wide-band models constructed from the spectral lines, and on a simpler level, the gray gas representation of the molecular spectrum can be considered. The simplest treatment for the case of enclosure fire is to consider the gas to be a gray gas of prescribed constant absorption coefficient. Narrow Band ModelA well known narrow band model is that proposed by Grosshandler and Modak (GrosshandlerWL:1981), which is based on the statistical model by Goody (GoodyRM:1964) for tri-atomic molecules with equal line strengths within each narrow band region, and with homogeneous effects accounted for through the Curtis-Godson approximation which employs suitable averages along a line-of-sight. For hydrogen flame, the five gas bands of the H2O, the main combustion products in the infrared region (1-6 μm) are considered which are 1.14 μm, 1.38 μm, 1.87 μm, 2.7 μm and 6.3 μm. For flames involving mixtures of hydrogen and hydrocarbon (e.g., hydrogen flame diluted by CH4), band overlap is also taken into account for multiple bands and mixture of CO2, H2O, CO and CH4 gases, particularly for 4.3 μm of CO2, 2.3 μm and 3.3 μm of CH4, and 4.7 μm of CO. Wide Band ModelEdwards and Balakrishnan (EdwardsDK:1973) developed a spectral version of exponential wide band model, which is based on the fact that the absorption and emission of radiation by a molecular gas is concentrated in between one and six vibrational bands. Within these bands, the spectral lines associated with rotational modes of energy storage are reordered in wave number space with exponentially decreasing line intensities moving from the band head. The band shape is then approximated by one of the three simple exponential functions, with radiative properties of each absorption band obtained from specified model parameters. Grosshandler’s Total Transmittance, Non-Homogeneous (TTNH) ModelThe total transmittance, non-homogeneous (TTNH) model for CO2 and H2O mixture is based on total transmittance data for homogeneous systems, with effective pressure-path lengths and temperatures for non-homogeneous systems taken as gas concentrations weighted averages along a line-of-sight (GrosshandlerWL:1980). Mixed Gray Gas ModelThe most popular mixed gray gas model for modeling combustion products (including soot) from fires is that proposed by Truelove (TrueloveJS:1976), which is based on representing the banded spectra of CO2 and H2O as a mixture of clear and gray gases. The total emittance of the combined emissions of the CO2 and H2O vapors was obtained by Truelove by fitting the spectral data of the gases as gray gas mixture of one clear and three gray gases. Banded Mixed Gray Gas ModelTruelove’s mixed gray gas model, employing one clear and three gray gas representations, can be written in a banded form where, for a given model spectrum, the gray gas weightings are determined as the fractional amount of black body energy in the spectral regions where “gray gas absorption coefficients” exist (ModestMF:1991). Recently, Cumber and Fairweather (CumberPS:1999) have improved the method by incorporating CO and CH4 emissions. Expressing total absorptivity and emissivity of a gas in terms of the weighted-sum of gray gases are useful, especially for the zonal method of analysis of radiative transfer. Invalid BibTex Entry! Physiological Impact
Skin contact with liquid hydrogen or cold hydrogen gas may cause severe cold burns, comparable with those caused by boiling water. Unprotected skin may freeze onto surfaces cooled by the liquid, causing severe damage on removal. Prolonged skin exposure to cold hydrogen may result in frostbite. A symptom is local pain which usually gives warning of freezing but sometimes no pain is felt or it is short-lived. Frozen tissues are painless and appear waxy, with a pale whitish or yellowish colour. Thawing of the frozen tissue can cause intense pain. Shock may also occur. The eyes are particularly susceptible – even small splashes of liquid hydrogen, or short exposures to cold vapor or gas, may cause instant freezing of eye tissues and permanent damage. Transient exposure to very cold gas produces discomfort in breathing and can provoke an attack of asthma in susceptible people. Prolonged inhalation of cold vapor or gas may cause serious lung damage. Prolonged exposure of the entire body to cold can result in hypothermia. Hydrogen is not poisonous, but as with any gas (except oxygen) a risk of asphyxiation exists mainly in confined areas as a result of oxygen depletion. Normal air contains around 20.8 % of oxygen, by volume. Besides the dilution by mixing with other gases, oxygen may be consumed in combustion of hydrogen or other burning gases and may be depleted via condensation on very cold surfaces like liquid hydrogen pools. Thus diluting the oxygen volumetric content below 19.5 % will cause effects on human beings. Alarm levels are generally set at 19 % oxygen. This is less than 2 % below normal levels, so it is important that sensors are stable in order to avoid false alarms. The different stages of asphyxiation at ground level are related to the remaining oxygen concentration as shown in the following table. Table: Asphyxia – Effect of O2 Concentration from NASA (NASA:NSS:1740:16:1997), partially accomplished and synchronized with DNV data (DNV:2001).
Invalid BibTex Entry! Direct Blast EffectsThese direct effects, also called primary effects, are caused by the dynamic pressure waves. Although the human body is able to adapt to slow pressure changes (diving, high altitudes, etc.) the dynamic changes in a blast front may cause severe damage. Those organs, where large differences in densities are encountered, like the lunge or the inner ear, are particularly vulnerable. Ear damage is not leading to death, but due to the ears’ high sensitivity it is often used as an indicator for an exposure. Lunge damage is depending on a combination of peak overpressure Ps and on the pulse duration tp (Fig. 1).  Fig. 2: Threshold data from Baker, NASA, and gaseous detonation data ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=BakerWE:1983 | BakerWE:1983) (NASA:NSS:1740:16:1997) (DorofeevSB:1996a)]] Similar as for the structural effects threshold limits for ear and lunge damage are displayed in pressure-impulse diagrams (Fig. 2). However, as impulse and pressure are correlated, the coordinates pressure and pulse duration provide a clearer and decoupled view. The transformed data are given in Fig. 3. Not only for the general mixing and detonation initiation but also for the physiological effects the spatial confinement is a very important factor. Generally one has to expect an increased immediate and late mortality in closed space blast scenarios compared to open-air explosions (KlugerY:2003) (KaiserW:2002). However, usually only little mortality is due to these primary effects compared to the more severe combination of indirect blast effects, like missiles, body translation and associated impact and heat effects. Indirect Blast EffectsIndirect blast effects include secondary effects, these are generated by missiles (e.g. accelerated parts of the pressure vessel, parts of the building, glass, etc.) and tertiary effects linked to the body translation. Especially the impact, the deceleration when hitting a wall or any other a solid structure, can cause skull fractures with traumatic consequences, even death. With a simplified model the body displacement caused by the blast may be calculated and a lethality threshold may be attributed to the resulting velocities, see [Baker 1983]. See figures 1 and 2 with the skull fracture as the representative indirect blast effect. Invalid BibTex Entry! Thermal effects from fires are also called quaternary effects. Basically there are two phenomena linked with hydrogen fires which could harm human beings: elevated air temperature and heat radiation. Depending on the scenario only one of both or a suitable combination has to be considered. Elevated Air Temperature Effect Time to incapacitation as a function of the air temperature ([[http://hysafe.org/wiki/BRHS/OFD-Chapter4?action=bibentry&bibfile=DB&bibref=CPR16E:2005:GreenBook | CPR16E:2005:GreenBook)]] Below 70°C, no severe effect has to be expected. Between 70°C and 150°C the time to incapacitation may be 94 minutes and 6 minutes, respectively (CPR16E:2005:GreenBook). The figure shows a plot of the empirical dependency. Other physiological responses are summarized in the following Table 1: Table 1: Elevated Air Temperature Effects
Above 150°C, the radiation effect becomes the dominant factor. Heat Radiation EffectHeat radiation may cause pain, first, second and third degree burns as well as fatal burns. The different burn types are characterised by the depth they reach in the skin. Similar as for the pressure effects a combination of the peak load, here radiation intensity, and the characteristic duration are the most important factors. Above 1.6 kW/m2, negative effects on human beings have to be expected. Table 2 relates exposure times and pain thresholds: Table 2: Threshold of Pain (KaiserW:2002)
The fatality rate may be calculated by use of probit functions. Prominent probit functions are the Eisenberg functions and the TNO functions. The first is based on nuclear radiation, the second on the radiation of hydrocarbon fires. So, both are not directly applicable to hydrogen fires. Potential knowledge gap: suitable probit function The following Table 3 based on the TNO probit function relates the exposure time and the radiation intensity for 100 % fatality: Table 3: Maximum Radiation Exposure Time (DNV:2001)
Besides the infrared content hydrogen combustion produces UV radiation capable of sunburn-like effects. Hydrogen fires are difficult to see at daylight and due to the optical properties the heat of smaller flames is felt late. Invalid BibTex Entry! Using the appropriate protective equipment can reduce the possible consequences of the above described hazards. The concerned personnel should be protected against exposure to cryogenic temperatures, high temperatures, thermal radiation from a hydrogen flame, and oxygen-deficient atmospheres. Procedures that are established for operations involving hydrogen should describe the personal protective equipment (PPE) that is needed for the operations to be performed. Some general guidelines for PPE that should be considered beneficial in working with hydrogen are summarized below. These guidelines do not address PPE that should be considered when involved in other activities such as working on electrical circuits or performing a cleaning or decontamination operation. Some specific recommendations for PPE are:
The immediate treatment of persons which came in contact with liquid hydrogen or have been exposed to the very cold gases is to loosen any clothing that may restrict blood circulation and seek immediate hospital attention for all but the most superficial injuries. Do not apply direct heat to the affected parts, but if possible place in lukewarm water. Sterile dry dressings should be used to protect damaged tissues from infection or further injury, but they should not be allowed to restrict the blood circulation. Alcohol and cigarettes should not be given. Environmental Impact(:include BRHS(.EffectOnTheEnvironment) << | Content | >> |