
|
BRHS /
Combustion of HydrogenBRHS.GroupHeader self=0 basepage={*BRHS.OFD-CombustionOfHydrogen} Premixed combustion of hydrogen-air mixturesLaminar premixed flamesStructure of the reaction zone and flame temperature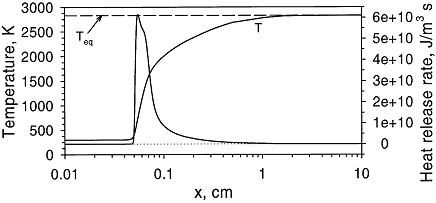 Figure 1. Distributions of temperature and heat-release rate in the \mathrm{H_2}-\mathrm{O_2} flame. From Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002). The study of the laminar flame structure is of fundamental interest in combustion science. It is also a necessary first step towards understanding combustion processes. In turbulent combustion, for example, there are many occasions where chemical reactions are localised in laminar flames that are being wrinkled and perturbed by turbulence. While entire monographs have been devoted to detailed experimental studies of the structure (e.g Fristrom (1995) (FristromRM:1995)) there appears to be no focus on hydrogen combustion. Studies of the flame stucture are quite difficult as laminar flames are very thin and complex. 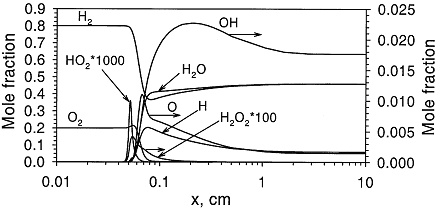 Figure 2. Distributions of mole fraction of species in the \mathrm{H_2}-\mathrm{O_2} flame. From Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002). The internal flame structure is known to depend on the chemical kinetics of the combustion reactions, and, thermodynamic as well as transport properties of all species in the flame. Solutions of the conservation equations of mass, energy and chemical species by means of numerical codes (e.g. Kee, Rupley & Miller (1987) (KeeRJ:1987) and Kee, Rupley & Miller (1989) (KeeRJ:1989)) are being used to resolve the details of the flame structure. The thermo-chemical and transport properties of the species are included via databases into the codes. The reaction mechanisms used in the simulations are taken from separate studies. An example of results obtained in this way is given by Figure 1 and Figure 2, showing distributions of temperature, heat release and species concentrations in a rich \mathrm{H_2}-\mathrm{O_2} premixed flame with an equivalence ratio of 2 at atmospheric conditions (after Liu, Guo, Smallwood & Gulder (2002) (LiuF:2002)). A characteristic feature of the heat release in the flame is its sudden start caused by the chain branching reaction \mathrm{O} + \mathrm{H_2} \rightarrow \mathrm{H} + \mathrm{OH}
initiated by the rate limiting reaction \mathrm{H} + \mathrm{O_2} \rightarrow \mathrm{O} + \mathrm{OH}
having an activation energy of about 17 kcal/mole. Very quickly after the start of the chain branching reactions a high concentration of radicals is reached within the flame followed by a slow and extended, three molecular radical recombination zone where reactions like \mathrm{H} + \mathrm{OH} + \mathrm{M} \rightarrow \mathrm{H_2O} + \mathrm{M}
\mathrm{H} + \mathrm{H} + \mathrm{M} \rightarrow \mathrm{H_2} + \mathrm{M}
\mathrm{O} + \mathrm{O} + \mathrm{M} \rightarrow \mathrm{O_2} + \mathrm{M} \quad \text{etc.}
lead to final equilibrium. The heat relase during the conversion from reactants to products causes the temperature to rise (see Figure 3). 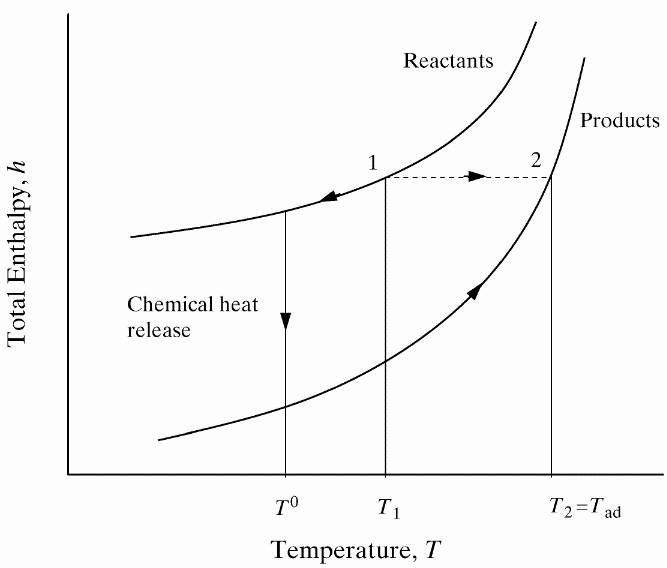 Figure 3. The principle of energy conservation during the conversion of reactants into products during combustion. From Law (2006) (LawCK:2006a). In the absence of heat losses to the surroundings, the final temperature attained is called the adiabatic flame temperature, T_f^{\scriptsize \text{ad}} (see Figure 3). More specifically, if a given uniform mixture with an initial temperature and composition is made to approach chemical equilibrium through an adiabatic, isobaric process at pressure P, then the final temperature is called the adiabatic flame temperature, T_f^{\scriptsize \text{ad}} (see page 37 of Law (2006) (LawCK:2006a)). When an adiabatic combustion process is isochoric instead of isobaric, i.e. when the volume occupied by the product mixture equals that of the reactant mixture prior to combustion, the final flame temperature T_f^{\scriptsize \text{ad,cv}} is larger than T_f^{\scriptsize \text{ad}}. The larger value of T_f^{\scriptsize \text{ad,cv}} stems from the fact that no work is done on the surroundings during isochoric combustion. All energy released by the chemical reactions is invested in raising the temperature of the mixture. Conversely, during isobaric combustion the hot product gases have to displace the surrounding air for the pressure to remain constant. A portion of the energy released by the chemical reactions that is consumed to displace the surroundings becomes unavailable for heating the mixture. 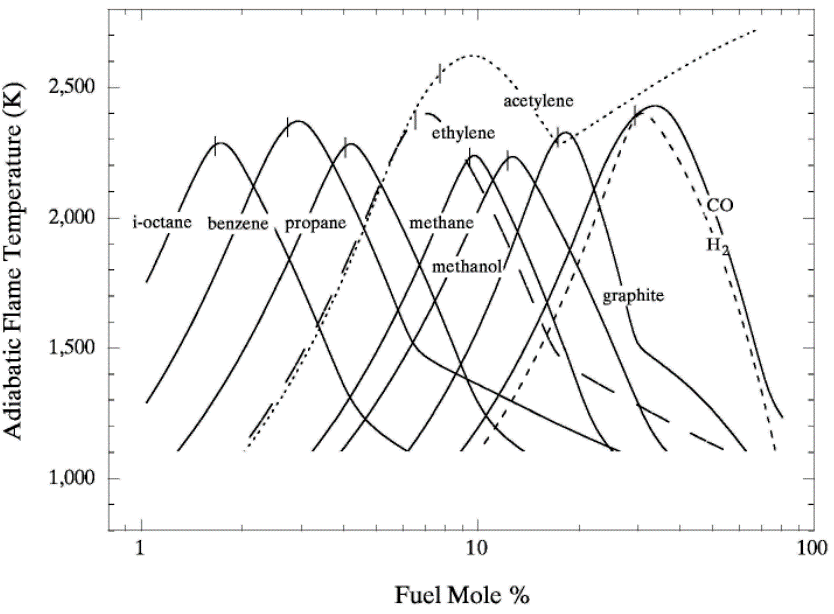 Figure 4. Adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of the mole percent of fuel for several fuel–air mixtures at initial conditions of 1 bar and 298.15 K. The vertical bars indicate stoichiometric concentrations. From Law (2006) (LawCK:2006a). Figure 4 illustrates the behaviour of the adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of mixture composition for a variety of fuels mixed with air. With all fuels the following trend is observed: the adiabatic flame temperature attains a maximum at a fuel concentration slightly above the stochiometric value, and levels off as the fuel concentration approaches the flammability limits. When T_f^{\scriptsize \text{ad}} is plotted against the fuel concentration, the locations of the flame temperature curves are seen to be scattered along the the horizontal axis. However, when these curves are plotted against the equivalence ratio, as is done in Figure 5, their apearance becomes more systematic because the stoichiometric concentration of all fuels coincide at \phi=1. The flame temperature curves are also seen to behave in a manner that allows them to be expressed by matematical relationships as a function of the equivalence ratio \phi=1. For fuel-lean mixtures at moderate pressures and temperatures of up to 2300 - 2400 K, the dissociation of product species is negligible and the product composition can be estimated from the overall chemical equation. This makes the calcualtion of the adiabatic flame temperature easier. Furthermore, the adiabatic flame temperature can approximated by simple formulas like the one developed by Chang & Rhee (1983) (ChangSL:1983) in the form: T_f^{\scriptsize \text{ad}} =a\cdot \left[1+b\cdot \mathrm{ln} \phi +c\cdot \left(\mathrm{ln} \phi \right)^{2} \right]
where
In the above expressions P, \phi and m respectively denote the pressure, equivalence ratio and mass. The coefficients for hydrogen-air mixtures are: a_{1} =2412.2 K; a_{2} = 17.9 K; b_{1} = 0.473 K; b_{2} = 0.021 K; c_{1} = 0.0217 K; and c_{2} = 0.0191 K. 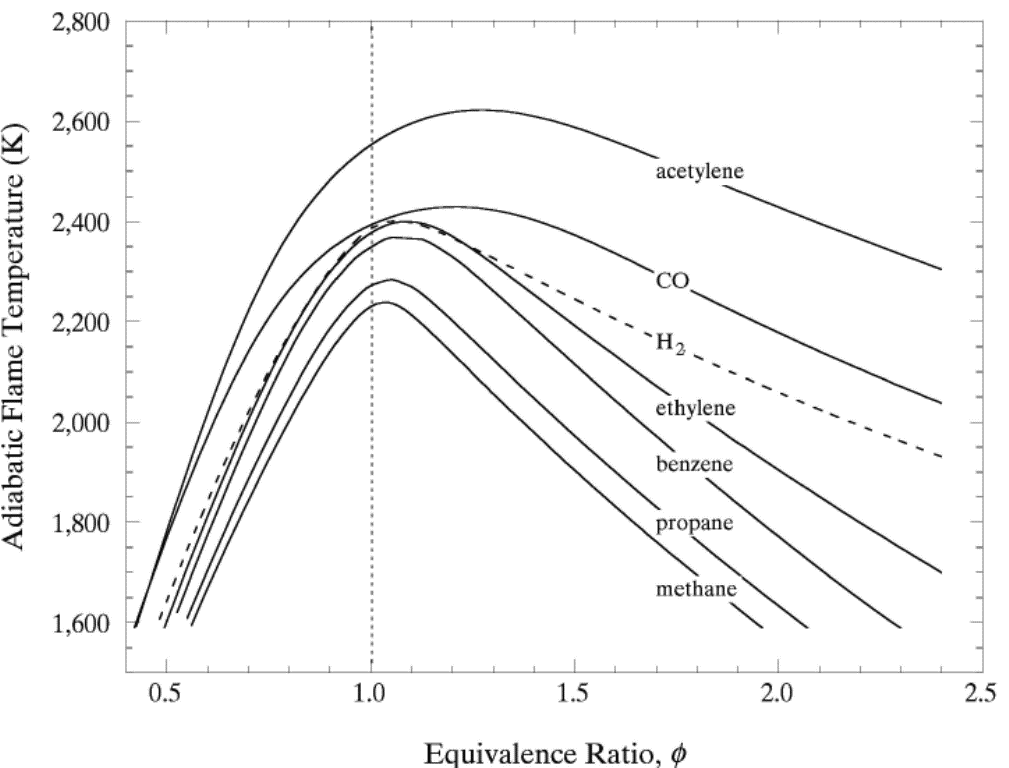 Figure 5. Adiabatic flame temperature, T_f^{\scriptsize \text{ad}}, as a function of fuel equivalence ratio, \phi, for several fuel–air mixtures at initial conditions of 1 bar and 298.15 K. From Law (2006) (LawCK:2006a). At higher pressure and temperature, and, with rich mixtures, the product mixture contains many more species because of dissociation. The composition of the products can then only be estimated by large reaction sets. Specialised chemical equilibrium codes then become a necessity to compute the adiabatic flame temperature. Bibliography Chang S.L. and Rhee K.T. (1983) Adiabatic flame temperature estimates of lean fuel/air mixture. Combustion Science and Technology, 35:203-206.(BibTeX) Laminar burning velocity and laminar flame thicknessLaminar flames propagate via the diffusion of heat and free radicals from the reaction zone to the unburned mixture ahead of it to effect ignition. The diffusion flux depends on the temperature gradient (which in turn depends on the reaction rate) and the various transport coefficients for the different species. The pressure remains practically constant across a laminar flame, hence the flame temperature corresponds closely to the product temperature for a constant pressure adiabatic process. The quantitative description of a laminar flame requires a detailed knowledge of the chemical kinetics, transport coefficients, and the thermochemical data of the various chemical species involved in the reactions. Thus, the laminar burning velocity provides a fundamental parameter whereby one can assess one's knowledge of the combustion process of a given explosive mixture. There are various methods for the experimental measurement of the laminar burning velocity but each has certain advantages and disadvantages. 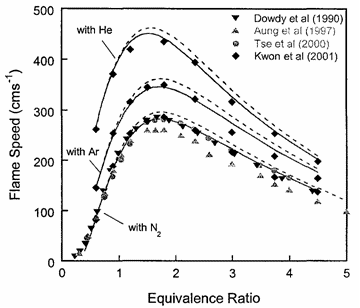 Figure 1. Laminar flame speed at 298 K and 1 atm for \mathrm{H_2}-\mathrm{O_2} mixed with \mathrm{N_2}, \mathrm{He} and \mathrm{Ar} (\mathrm{O_2}:\mathrm{N_2} = \mathrm{O_2}:\mathrm{He} = \mathrm{O_2}:\mathrm{Ar} = 1:3.76). From Lee (2006) (LeeJHS:2006). The solid and dashed lines are predicted values obtained with chemical kinetic mechanisms. Since the laminar burning velocity depends on curvature and flow straining, the correct laminar burning velocity is often difficult to determine. Flame instability also adds to the difficulty of the experimental measurement of the laminar burning velocity especially in the composition range where the flame is cellular. Theoretical computation of the laminar burning velocity is possible provided that the flame chemistry, transport coefficients and the thermochemical data are known. There are standard computer codes (e.g. CHEMKIN) available for such purposes. In general, the weakest link is usually associated with the inadequate modelling of the detailed flame chemistry. In fact, experimental burning velocity data is used to validate theoretical models of the detailed flame chemistry. For hydrogen-oxygen mixtures, the flame chemistry is perhaps the most well-established compared to the other common hydrocarbon fuels. A comparison between theoretical and experimentally measured values is given in Figure 1 for hydrogen-oxygen mixtures using various inert diluents (i.e. argon, helium, and nitrogen). The excellent agreement indicates that the chemistry of hydrogen-oxygen flames is now quite well-established. In Figure 1 it is also seen that the maximum laminar burning velocity for hydrogen-oxygen-nitrogen (or -air) mixtures is about 300 cm/s which is approximately six times that of most of the common hydrocarbon fuels of the order of 40 cm/s. This is a result of the high diffusivity of hydrogen, accounting for the shift of the maximum burning velocity towards richer mixtures. For the common hydrocarbon fuels, the maximum burning velocity occurs at just slightly richer than stoichiometric composition. It should be noted that laminar flame models also provide the fundamental basis for the modelling of turbulent flames. Also, a good understanding of the flame chemistry is essential to the choice of inhibitors for the suppression of explosions. For hydrogen-oxygen mixtures the flame chemistry is adequately known (Lee (2006) (LeeJHS:2006)). The magnitude of the laminar burning velocity is determined experimentally. Techniques of measuring flame velocity may be categorised as folows:
The advantages and disadvantages of these methods have been described by Koroll, Kumar & Bowles (1993) (KorollGW:1993):
A rudimentary way to estimate the laminar flame thickness rests on the assumption thatflame propagation is driven by heat conduction only (PoinsotT:2001): \delta_L = \frac{\lambda_u }{\rho_u {C_\mathrm{P}}_u} \frac{1}{{S_u}_L}
Here \delta_L denotes the laminar flame thickness; \lambda_u, \rho_u and {C_\mathrm{P}}_u} respectively denote the thermal conductivity, density and specific heat of unburnt (fresh) mixture; and, {S_u}_L the laminar burning velocity. Estimates obtained in this manner have been found to underestimate the real flame thickness by a factor of five. Similar expressions to estimate the laminar flame thickness have also been proposed by Blint (1986) (BlintRJ:1986) (see pages 57 and 58 of Poinsot & Veynante (2001) (PoinsotT:2001)).  Figure 2. Definition of the laminar flame thickness. From Poinsot & Veynante (2001) (PoinsotT:2001). More accurate values for the laminar flame thickness may be obtained from the numerical solution of the governing equations applied to the flame structure. An example of flame thickness of hydrogen-air mixtures obtained in this manner is by Aung, Hassan & Faeth (1997) (AungKT:1997). These authors report the following magnitudes for the unstretched laminar flame thickness \delta_L^{\circ} at normal temperature and pressure: \delta _L^{\circ} = 0.65 mm for equivalence ratio \Phi = 0.40 ; \delta _L^{\circ} = 0.35 mm for \Phi = 0.70 and \delta _L^{\circ} = 0.43 mm for \Phi = 4.0 . The unstretched laminar flame thickness \delta_L^{\circ} is defined as follows (Poinsot & Veynante (2001) (PoinsotT:2001)) and illustrated by Figure 2: \delta_L^{\circ} = \frac{T_2-T_1}{\mathrm{max}\left(\left|\partial T/\partial x\right|\right)}
There is also another laminar flame thickness as illustrated by Figure 2: the total thickness \delta _L^{\scriptstyle \mathrm{t}} . This quantity is defined as the distance over which the reduced temperature \theta = (T - T_1)/(T_2 - T_1) changes from 0.01 to 0.99; but this quantity is not very useful for modeling purposes (Poinsot & Veynante (2001) (PoinsotT:2001)). Its definition creates a long temperature tail which does not correspond with the species profiles across the flame structure. Aung K.T., Hassan M.I. and Faeth G.M. (1997) Flame stretch interactions of laminar premixed hydrogen/air flames at normal temperature and pressure. Combustion and Flame, 109:1-24.(BibTeX) Flame stretch and effect of flame curvature, Markstein lengthsFlame front propagation in a non-uniform flow is affected by strain and curvature effects, which lead to the change in the flame area and measured by flame stretch, which is a fractional rate of change of a flame surface element: k = \frac{1}{A}\frac{{dA}}{{dt}},
where k \ - flame stretch, A – area of the flame surface element, t - time. Asymptotic theories, e.g. (MarksteinGH:1964), (WilliamsFA:1985), (ClavinP:1985) suggest that the flame stretch (flame strain, or flame curvature, or both) may affect the laminar burning velocity and in the limit of the small stretch it controls the laminar burning velocity through the linear relationship: s_u = s_{u\infty } - L\,k, \ \ \ \ \ \ \ \ (1)
where s_u - laminar burning velocity, s_{u\infty } - laminar burning velocity of planar unstretched flame, L – Markstein length, k - stretch rate. The above expression is often recast in the following form: \frac{{s_u }}{{s_{u\infty } }} = 1 - Ma \cdot \frac{{k\delta }}{{s_{u\infty } }} = 1 - Ma \cdot Ka , \ \ \ \ \ \ \ \ (2)
where Ma=L/\delta - Markstein number, \delta = {{\lambda _u } / {\left( {\rho _u \,c_p s_{L\infty } } \right)}} - characteristic flame front thickness, Ka = k \delta / s_{u\infty } - Karlovitz number. Formally a linear dependence between the burning velocity s_u and the stretch rate k , which is a result of a theoretical analysis, is valid only for small stretch rates ( Ka << 1 ). In fact, a non-linear relationship between and k is found for a broader range of k (AungKT:1997). 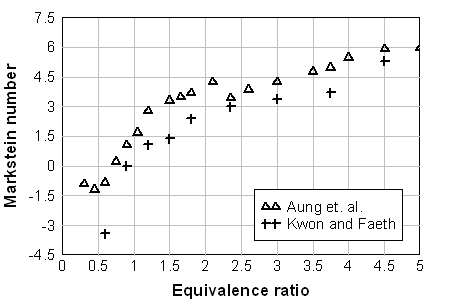 Fig. 1. Markstein number of the hydrogen-air flame at normal pressure and temperature as a function of the equivalence ratio \Phi . (AungKT:1997), (KwonOC:2001). The sign of the Markstein length (Markstein number) controls the preferential-diffusion stability of the laminar flame fronts. Equations (1), (2) readily demonstrates the relationship between the stretch and preferential-diffusion instability: if the Markstein length (Markstein number) is negative then the laminar burning velocity increases as the flame stretch increases. This causes bulges in a flame front with a positive stretch to grow further and thus the flame is unstable. If the Markstein number is positive, then the laminar burning velocity decreases with increasing stretch and similar bulges in the flame surface become smaller, so that flame become stable to preferential-diffusion instability. Hydrogen flames are unstable in learn mixtures. Figure 1 shows the Markstein number of H2-air flames as a function of the equivalence ratio \Phi ; at normal temperature and pressure reported in (AungKT:1997) and (KwonOC:2001). The neutral preferential-diffusion condition is at equivalence ratio \Phi=0.7-0.9 . With increase of pressure the Markstein length L becomes positive at larger equivalence ratios (KwonOC:1992), (TseSD:2000). Markstein length of H2-air flames was reported in (DowdyDR:1990), where it changed from about –0.4 mm at \Phi=0.3\ (~10% H2) and up to 0.5 mm at \Phi=2.3\ (~68%). Poinsot T. and Veynante D. (2001) Theoretical and numerical combustion. Edwards, Philadelphia.(BibTeX) Flame cellular structure and wrinklingDuring experimental measurements of the H2-air burning velocities three kind of instabilities, leading to appearance of flame wrinkling, were usually observed: preferential-diffusion instability (when Markstein length L and Markstein number Ma are below zero), hydrodynamic instability and buoyant instability (AungKT:1997), (KwonOC:2001). The preferential-diffusion instability creates irregular (chaotic) distortion, leading to formation of irregular flame surface, larger flame front area and faster propagation of the stretched flames. Under the stable preferential-diffusion conditions propagation of the initially smooth flame front is followed by onset of the regular cellular structure, formed by hydrodynamic instabilities. Detailed review and analysis of the hydrodynamic instabilities in the spherically propagating premixed flames are given in the work by Bradley and co-workers {[DB, BradleyD:1994b]}, (BradleyD:1999), (BradleyD:2000). They considered a spherical premixed flame as a fractal surface, formed by the hydrodynamics instabilities. Hydrodynamic instability appears first as a cracking of the flame surface, then followed by development of a cellular flame structure and flame wrinkling. As the flame propagates the wrinkling increases and creates a larger surface area and consequent flame acceleration. As a result, the flame speed increases as a square root of elapsed time. If a flame radius is large enough, the turbulent flame appears. According to Bradley (BradleyD:1999) hydrodynamic instabilities arise at the larger wavelengths and cascade down through a range of ever decreasing wavelengths to be stabilised at the smallest wave-length by thermo-diffusive effects. The largest instability is bounded only by the physical scale of the problem and the outer cut-off is expected to be of the order of the flame front radius. The inner cut-off of is expected to be of the order of the real flame front thickness. Semi-empirical correlation is given in (BradleyD:1999) for the critical Peclet number Pe_{cl} , characterising the onset of cellular structure for freely propagating flames: Pe_{cl} = 177Ma+2177 for -5 <Ma<8 , where Pe=r s_u / \nu_u - Peclet number, r - flame radius, s_u - burning velocity, \nu_u - kinematic viscosity of unburnt (fresh) mixture. It is possible to show that for a wide range of mixtures the onset of instabilities occurs at a flame radius of order 10 cm and the minimum cell size is below 1 cm. Conclusions of this analysis can be applied only to the stable preferential-diffusion conditions. The flames with unstable preferential- diffusion conditions do not have the coherent cellular structure and the mechanism of their surface distortion cannot be explained by hydrodynamic instability alone (KwonOC:1992).  Fig. 1. Shadowgraph of the H2/O2/N2 flame surface for stable preferential-diffusion conditions ( \Phi=3.27 ). Left image for Pe > Pe_{cl} ; right image for Pe > Pe_{cl} .  Fig. 2. Shadowgraph of the H2/O2/N2 flame surface for unstable preferential-diffusion conditions ( \Phi=1.00 ). Left image for Pe > Pe_{cl} ; right image for Pe > Pe_{cl} . The characteristic flame shape, corresponding to the thermodiffusively stable and unstable flames, is shown in Fig.1, 2, adopted from (KwonOC:1992) (with permission). Freely propagating flames are subject to natural convection. Analysis of convection instabilities was conducted by Babkin et. al. (BabkinVS:1984). It was demonstrated that the natural convection deforms the flame front in the case when the Froude number is above the critical value: Fr = {{s_u^2 } / {\left( {g\,D} \right)}} > 0.11,
where D is the critical diameter of the flame front. Under effect of natural convection the flame front initially becomes flatter at the lower part, the flame front rises as a whole in upward direction. Then the lower flat part of the flame bends inside, forming vortical flame structure. The fluid flow around naturally convected vortical flame creates the flame stretch, which is known to suppress formation of the cellular structure and flame wrinkling due to hydrodynamic instabilities. Aung K.T., Hassan M.I. and Faeth G.M. (1997) Flame stretch interactions of laminar premixed hydrogen/air flames at normal temperature and pressure. Combustion and Flame, 109:1-24.(BibTeX) Dependence of burning velocity on hydrogen concentration, pressure and temperatureDahoe (DahoeAE:2005) gives an extensive comparison of the laminar burning velocities of hydrogen mixtures, obtained in (LawCK:1993), (TakahashiF:1983), (WuCK:1984), (IijimaT:1986), (DowdyDR:1990), (EgolfopoulosFN:1990), (KorollGW:1993), (VagelopoulosCM:1995), (AungKT:1997), (TseSD:2000), (KwonOC:2001), (LamoureuxN:2002). Dependence of the laminar burning velocity on equivalence ratio (H2 concentration) at normal pressure and temperatures T = 293 - 298 K , adopted from (DahoeAE:2005), is shown in Figure 1. 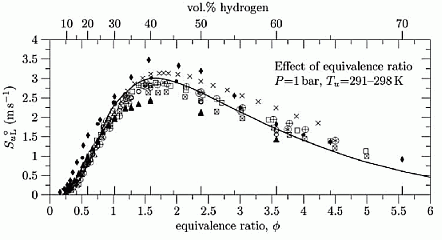 Figure 1. Effect of hydrogen concentration (expressed in equivalence ratio) on the laminar burning velocity of hydrogen–air mixtures, reproduced from (DahoeAE:2005) (with permission). The H2 combustion has a unique combustion properties:
Accurate measurement of H2 burning velocity is not possible for concentrations below downward flame propagation limit 9% of H2 since anisotropic flame propagation occurs in near-limit mixtures (KorollGW:1993). Liu and MacFarlane (LiuDDS:1983) obtained burning velocities within steam concentration range 0-15%. An empirical correlation by Liu and MacFarlane developed to describe the H2-air-steam burning velocity as a function of hydrogen concentration, steam concentration and temperature, is given below: s_u = BT_u ^C \exp \left( {D\,x_{H_2 O} } \right), \ \ \ \ \ \ \ \ \ (1)
where s_u – laminar burning velocity, m/s, B, C, D – coefficients, T_u – temperature of unburned gas in K, x - volumetric fraction of the species (H2 – hydrogen, H2O - steam). Coefficients for the correlation are given in Table 1. The reported root mean square deviation of the correlation is 0.189 m/s. The authors suggested that the correlation may be applied in the whole range of hydrogen flammability limits 5-75% volume and steam concentration range 0-25% volume; experimental temperature range was 293-523K. Reported by the authors root mean square deviation of the correlation is 0.189 m/s. They suggested that the correlation may be applied in the whole range of hydrogen flammability limits 5-75% and steam concentration range 0-25%; experimental temperature range was 293-523K. 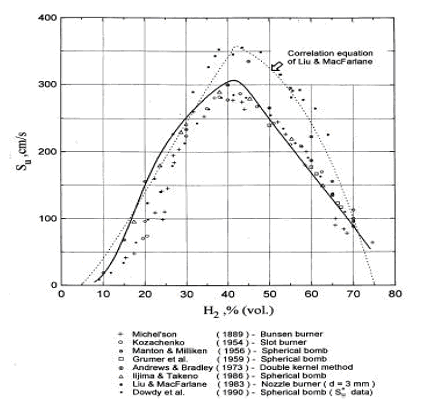 Figure 2. Laminar burning velocity of hydrogen air mixtures at room temperature and atmoshpheric measured by various methods. Solid line computed values for spherical flame propagation; dotted line correlation equation of Liu and MacFarlane. Table 1. Coefficients in the burning velocity correlation, eq. (1).
Combustion of H2-air-steam mixtures was studied later by Koroll et. al. (KorollGW:1993) within a steam concentration range 12-42% and Lamoureux et. al. (LamoureuxN:2002), who measured burning velocity with steam concentrations 10, 20, 30%. Koroll et. al. developed a correlation for burning velocity of H2-O2-diluent and H2-O2-diluent/steam mixtures, which is applicable in H2 concentration range 9% - 70%. Burning velocity of H2-O2 mixtures and hydrogen-fuelled mixtures with diluents were studied by Kwon et. al (KwonOC:1992) - H2-O2-N2 mixtures, Koroll et. al. (KorollGW:1993) - H2-air-diluent mixtures (normal pressure and temperature, hydrogen concentration range 9-70%, empirical correlation for S_u is given), Tse et. al. (TseSD:2000) - H2-O2-diluent mixtures, Kwon and Faeth [[DB, KwonOC:2001]} - H2-O2-diluent mixtures. Effect of steam and combined (CO2 + He) diluent on the burning velocity was studied in (LamoureuxN:2002) at T = 353K. Experimental data on the burning velocity at elevated pressures may be found in research by Iijima et. al. (IijimaT:1986), Kwon et. al. (AungKT:1997) – 3 atm, Tse et. al. (TseSD:2000) – up to 20 atm, Qin et. al. (QinX:2000) – up to 5 atm, Kwon and Faeth [[DB, KwonOC:2001]} – up to 3 atm, Kuznetsov et al. Invalid BibTex Entry! - up to 70 atm. Experimental data on the burning velocities at elevated temperatures are given by Liu and MacFarlane (LiuDDS:1983) – in the range 295K – 523K, Koroll et. al. (KorollGW:1993) – at temperatures 298K and 373K, Lamoureux et.al. (LamoureuxN:2002) – at temperatures 298K and 353K, Kuznetsov et. al. Invalid BibTex Entry! - at temperatures up to 573K. The cited studies used following experimental techniques. Optically accessed spherical flame propagation in a closed vessel was employed for velocity measurements in (DowdyDR:1990), (KwonOC:1992), (AungKT:1997), (TseSD:2000), (KwonOC:2001), (LamoureuxN:2002). In [DB, IijimaT:1986], (MiltonBE:1984), (DahoeAE:2005) the burning velocities were obtained using measurement in of pressure variation caused by confined deflagration in a windowless chamber. Double-kernel technique was used in (KorollGW:1993). Stabilised flames were used in (WuCK:1984) - stagnation flame and Bunsen burner, (EgolfopoulosFN:1990), (VagelopoulosCM:1995) - counterflow technique, (LiuDDS:1983) – constant velocity nozzle, (QinX:2000) – nozzle burner. Laminar burning velocities may be computed using fundamental kinetic and thermodynamic data. Comparison of the burning velocities predicted using different reaction mechanisms and software codes against experimental data may be found, e.g. in the papers (LiuDDS:1983), (EgolfopoulosFN:1990), (DowdyDR:1990), (VagelopoulosCM:1995), (AungKT:1997), (TseSD:2000), (QinX:2000), (KwonOC:2001), (LamoureuxN:2002), (DahoeAE:2005). 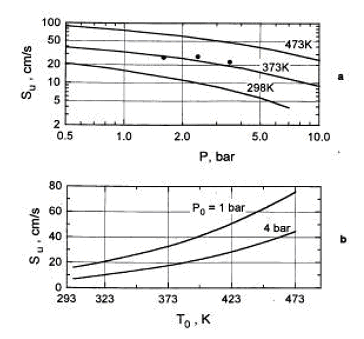 Figure 3. Laminar burning velocity as a function of pressure (a) and temperature (b) for 10% H2-air mixture (φ = 0.26.) The dependence of the laminar burning velocity on pressure and temperature is usually expressed as a polynomial function (PoinsotT:2001): s_u \left( {p,T} \right) = s_u \left( {p_0 ,T_0 } \right)\,\left( {\frac{p}{{p_0 }}} \right)^n \left( {\frac{T}{{T_0 }}} \right)^m,
where s_u \left( {p_0 ,T_0 } \right) - burning velocity at initial pressure p_0 and temperature T_0 , s_u \left( {p,T} \right) - burning velocity at actual pressure p and temperature T , m, n – temperature and baric indexes in dependence of the burning velocity correspondingly. In case, where combustion process may be assumed as adiabatic (e.g., spherical flame propagation in a closed vessel) and temperature changes only due to adiabatic compression, the dependence for the burning velocity may be expressed as a function of pressure only: s_u \left( {p,T} \right) = s_u \left( {p_0 } \right)\,\left( {\frac{p}{{p_0 }}} \right)^\varepsilon ,
\varepsilon = m_0 + n_0 - m_0 /\gamma _u - overall thermokinetic index, \gamma = {{c_p } / {c_v }} - specific heat ratio, c_p, c_v - specific heats at constant pressure and constant volume correspondingly. Values of baric, thermal and overall indexes, which may be recommended according to (BabkinVS:2003), are given in Table 2. The burning velocity increases rapidly with increase of temperature and just slightly - with increase of pressure (except for mixtures close the flammability limits). Table 2. Baric, thermal and overall thermokinetic indexes for H2-air laminar burning velocity ( p_0 = 1 atm, T_0 = 298K )
* - values in brackets are interpolated or extrapolated, ** - values determined in the range p=0.25-1.0 atm. In the range of H2 concentration 60-70% values n=(-0.4) – (-0.1) may be expected, (GrumerJ:1959). In paper by Iijina and Takeno (IijimaT:1986) following temperature and baric index values were reported: m = 1.54 + 0.026(\Phi - 1),
n = 0.43 + 0.003(\Phi - 1).
For stoichiometric mixture Dahoe (DahoeAE:2005) found following temperature and baric indexes using inverse problem method: m = 140.0 \pm 3.7 \cdot 10^{-2},
m = 194.0 \pm 4.4 \cdot 10^{-3}.
Dahoe A.E. (2005) Laminar burning velocities of hydrogen-air mixtures from closed vessel gas explosions. Journal of Loss Prevention in the Process Industries, 18:152-166.(BibTeX) Content: Fundamentals of hydrogen combustion Turbulent premixed flamesTurbulence scalesAlthough a huge number of theoretical, experimental and computational investigations on turbulence have been performed, the structure and description of turbulence still remain open issues. The motivation behind the study of turbulent flows is due to the fact that the vast majority of flows is turbulent and turbulence significantly increases the rates of transport and mixing of matter, momentum and heat in the flows (PopeSB:2000). Turbulence itself is a very complex phenomenon, involving different time and length scales. In the well-known energy-cascade theory, the kinetic energy enters the turbulence at the largest scales of motion through the production mechanism. This energy is transferred from the largest scale (integral scale) to smaller and smaller scales until it is dissipated by viscous action at the smallest scale, the so-called Kolmogorov length scale. The wide range of length-scales and time-scales, the production, the dissipation and the energy transfer between different length-scales make the modelling of turbulence one of the greatest scientific challenge. The level of difficulty in investigating premixed flames is greatly enhanced when also turbulence comes into play, because of the complex interactions between the turbulence itself and the combustion. The transfer rate of kinetic energy per mass unit of fluid over any particular scale between the macro structure and the micro structure obeys the relationship (this is known as Kolmogorov’s law), e.g., (BatchelorGK:1993): \varepsilon =-\frac{d}{dt} U_{}^{2} =A\frac{U_{}^{3} }{L} \ \ \ \ \ \ (1)
where A is a constant in the order of unity. Together with the root-mean-square of the instantaneous velocity fluctuations, this expression can be used to characterise the macro structure in terms of a macro velocity scale, a macro length scale and a macro time scale: u_{t} = u_{rms}^{,} \quad \quad \ell _{t} =\frac{{u_{rms}^{,}}^{3} }{\varepsilon } \quad \quad \tau _{t}^{} =\frac{{u_{rms}^{,}}^{2} }{\varepsilon }
The microstructure can be characterised by the Kolmogorov velocity, length and time scale: u_{K}^{} =\left(\nu \varepsilon \right)_{}^{1/4} \quad \quad \ell _{K}^{} =\left(\frac{\nu _{}^{3} }{\varepsilon } \right)_{}^{1/4} \quad \quad \tau _{K}^{} =\left(\frac{\nu _{}^{} }{\varepsilon } \right)_{}^{1/2}
where \nu denotes the kinematic viscosity. It should be noted that equation (1) describes the kinetic energy transfer on the larger scales as well as the viscous dissipation on the micro structure despite the apparent absence of the molecular viscosity. A combustion zone may also be characterised in terms of velocity, length and time scales. If the laminar burning velocity, the laminar flame thickness, and the chemical time scale: S_{u L} \quad \quad \delta _{L}^{} \quad \quad \tau _{c}^{} =\frac{\delta _{L}^{} }{S_{u L} } are taken as the fundamental scales of the combustion ((PetersN:1991), (BorghiR:1988)), the structure of a turbulent flame may be considered by relating these combustion scales to those of the turbulent flow field. The occurrence of a particular combustion regime is determined by the value of the Damkohler number: Da=\frac{L/U}{\tau _{c} } =\frac{\ell _{t} /u_{rms}^{'} }{\delta _{L} /S_{u L} } When the scales of the micro structure of the turbulent flow field are substituted for L and U, it constitutes the reciprocal Karlovitz number: Ka^{-1} =\frac{L/U}{\tau _{c} } =\frac{\ell _{K} /u_{K} }{\delta _{L} /S_{u L} } The Damkohler and Karlovitz number can be used to identify different combustion regimes [14, 15] by employing two dimensionless parameters, \left(\frac{u_{rms}^{,} }{S_{u L} } \right) and \left(\frac{\ell _{t}^{} }{\delta _{L}^{} } \right) and by rewriting their definitions into \frac{u_{rms}^{,} }{S_{u L} } = Da_{}^{-1} \left(\frac{\ell _{t}^{} }{\delta _{L}^{} } \right) (2) and \frac{u_{rms}^{,} }{S_{u L} } = Ka_{}^{2/3} \left(\frac{\ell _{t}^{} }{\delta _{L}^{} } \right)_{}^{1/3} (3) Since the expressions for the laminar burning velocity and the laminar flame thickness (DahoeAE:2003), \frac{S_{u L} }{S_{u L}^{o}} =\sqrt{\frac{\lambda (T_{u} )}{\lambda (T_{u 0} )} } \left(\frac{T_{u} }{T_{u 0}} \right)\left(\frac{P_{}^{} }{P_{0}^{} } \right)_{}^{\frac{n-2}{2} } \left(\frac{T_{f} }{T_{f}^{o} } \right)^{-\frac{n}{2} } \left(\frac{T_{f} }{T_{f}^{o} } \right)^{\frac{m}{2} } \exp \left[-\frac{Ea}{R} \left(\frac{1}{T_{f}} -\frac{1}{T_{f}^{o} } \right)\right] \frac{\delta _{L}^{} }{\delta _{L}^{o} } =\sqrt{\frac{\lambda (T_{u})}{\lambda (T_{u 0})} } \left(\frac{P }{P_{0}} \right)^{-\frac{n}{2} } \left(\frac{T_{f}}{T_{f}^{o} } \right)_{}^{\frac{n}{2} } \left(\frac{T_{f}^{} }{T_{f}^{o} } \right)_{}^{-\frac{m}{2} } \exp \left[+\frac{Ea}{R} \left(\frac{1}{T_{f}^{} } -\frac{1}{T_{f}^{o} } \right)\right] in conjunction with the definition of the thermal conductivity and the viscosity in terms of molecular properties imply that S_{u L} \delta _{L}^{} =\frac{\lambda }{\hat{C}_{P}^{} } =\frac{\mu }{\rho } a third relationship may be derived as \frac{u_{rms}^{,} }{S_{u L} } = Re\left(\frac{\ell _{t}^{} }{\delta _{L}^{} } \right)_{}^{-1} (4) Equations (2), (3) and (4) may then be used to construct a figure which is known as the Borghi diagram. Pope S.B. (2000) Turbulent flows. Cambridge University Press, Cambridge, United Kingdom.(BibTeX) Interaction between turbulence and flames: turbulent burning velocityAs if follows from the title a turbulent combustion is affected/dominated by the turbulence-chemistry interaction. The turbulence can promote the combustion by two main mechanisms: the larger turbulent length scales are capable of increasing the wrinkling of the flame, increasing the flame surface area and therefore the fuel consumption rate. If the Kolmogorov length scale of the flow is smaller than the flame thickness, the turbulence is also able to modify the inner flame structure, increasing the transport rate of heat and matter across the flame itself. It must be pointed out that in some cases turbulence decreases the combustion rate and it can even cause the quenching of the flame. Being the coupling between turbulence and chemistry a two way coupling, also the combustion affects the turbulent field. Across the flame, because of the heat release, a strong acceleration of the flow occurs, producing the so-called “flame generated turbulence”. Moreover the increase of temperature across the flame enhances the gas kinematic viscosity, damping the turbulence (relaminarization due to combustion).  Figure 1. Turbulent burning velocity. To expose the features of turbulent flame propagation, it is helpful to consider laminar flame propagation briefly. When a flame is stabilised in a laminar flow of combustibles, it establishes itself at a fixed position in the flow field and its surface remains smooth. In other words, it inherits the laminar behaviour of the flow field. Moreover, the velocity at which the cold reactants enter the flame zone in the normal direction, the laminar burning velocity, appears to be a mixture specific property. It reflects the sensitivity of the combustion process to changes in the chemical composition, fuel concentration, oxygen content, pressure and temperature of the reactants. By contrast, when a laminar flame becomes trapped within a turbulent flow of combustibles, it inherits the turbulent nature of the flow field: the turbulence of the approaching flow continuously distorts the flame and ceaselessly shifts its position in space between certain geometrical boundaries. As a result, the surface area of the instantaneous laminar flame changes in a chaotic manner, which is determined by the turbulence of the flow field. The geometrical boundaries between which the instantaneous flame front shifts its position are identified as a turbulent flame thickness. A superposition of many instantaneous flame surfaces results in a time-averaged picture that is frequently referred to as the turbulent flame brush, and inspired the definition of a turbulent burning velocity by analogy with the laminar burning velocity. Due to the enhancement of heat and mass transfer by turbulence, the turbulent flame brush propagates with a turbulent burning velocity that is greater than the laminar burning velocity. The local consumption of reactants at any particular portion of the flame surface, however, occurs within a zone whose width is equal to the local laminar flame thickness and at a rate which is determined by the local laminar burning velocity. In the case of large scale, low intensity turbulence, the instantaneous flame front will be wrinkled while the transport properties remain the same. The wrinkles increase the flame front area per unit cross section of the turbulent flame brush which results in a higher propagation velocity without a change in the instantaneous local flame structure itself. The instantaneous flame surfaces in such a turbulent flame are known as laminar flamelets. With this picture in mind, Damkohler and Schelkin derived the earliest models for the turbulent burning velocity. These authors and later Karlovitz demonsterated that turbulent flame speed is defined byz the level of turbulence. Damkohler G. NACA Tech. Memo 1112, National Advisory Committee for Aeronautics, Washington, 1947. Original: Z. Elektrochem., vol. 46, 1940, pp. 601. Borghi-diagram and interpretation of combustion regimesDepending on the ratio between the burning velocity and the flame thickness of the combustion zone, if a flame were to establish itself in a laminar flow of combustibles, and the velocity and length scales of the turbulent flow, there exist various modes of flame propagation. A flame may propagate as a reacting surface containing small scale wrinkles (wrinkled flame), as a surface containing large scale wrinkles (corrugated flame), the flame zone may be disrupted into an assembly of pockets containing reactants only, combustion products only, or a mixture of both (distributed reaction zones), or, it may be smeared out in space (well-stirred reactor regime). Each of these combustion regimes is known to have a specific burning velocity and flame thickness dependence on turbulence. 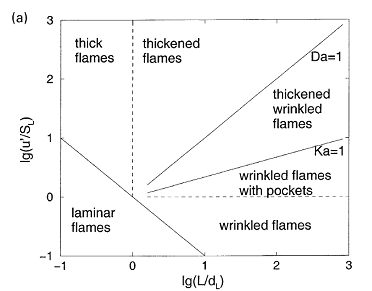 Figure 1. Borghi diagram of different combustion regimes The existence of different combustion regimes can be understood by considering the interaction between the turbulence scales and the instantaneous flame front, and with the aid of certain dimensionless groups that appear in the dimensionless form of the governing equations. A turbulent flow field is perceived to consist of a range of differently sized eddies with the macro structure and the micro structure as extremes. The eddies that form the macro structure are generated by the main flow. The Reynolds number associated with these eddies is so large that the effect of the molecular friction term in the momentum equation becomes negligible. As a consequence, the macro structure has an unstable nature (i.e. the character of the momentum equation is largely determined by the nonlinear convection term, and the large eddies ceaselessly break up into smaller ones. During this process of eddy break up the loss of kinetic energy due to viscous dissipation may be neglected. Each time a large eddy falls apart, its kinetic energy is carried on by the newly formed smaller eddies. The transfer of kinetic energy from larger to smaller eddies continues down to the micro structure, where the eddies are so small that molecular friction plays a significant role in the momentum and energy balance and the character of the momentum equation is dominated by the viscous term. Due to the consequential stability of the micro structure, the kinetic energy is no longer conveyed to smaller scales by the process eddy break up. Instead, the micro eddies convert their kinetic energy into heat. The described combustion regimes can be schematically represented on the 'turbulence intensityvs.turbulence length scale' diagram. Such diagram is used to call 'Borghi diagram' due to the name of the author who first introduced it. The lower left corner of the diagram is reserved for laminar flames. Although the precise value of Re is known to depend on the geometry of the flow domain (e.g. Re = 2000 in case of a tube; Re = 500 for the flow between two flat plates; Re = 0.1 for the flow around a spherical object), the boundary of this region is set at Re = 1. Due to the absence of turbulence scales, a flame stretch is the only interaction between the flow and the combustion. Among the remaining four regimes, the wrinkled and corrugated flames belong to the flamelet regime, which is characterised by Re > 1 (i.e. turbulence), Da > 1 (i.e. fast chemistry) and Ka < 1 (i.e. weak flame stretch). When Da > 1, and this condition covers the entire region of the distributed reaction zones as well, the time scale of the macro structure is large in comparison with the chemical time scale. This means that (i) the macro structure is not rapid enough to destroy the laminar flame structure to such a degree that the laminar burning velocity becomes an irrelevant parameter, and (ii) the chemistry is so fast that every change in the flame shape due to the large eddies is being reflected in the turbulent burning rate as the flame propagates normal to itself. Conversely, if the chemical time scale is smaller than the turbulence time scale, the flame may have changed its shape many times before any significant amount of reactants has been consumed. The flamelet regime is subdivided by a dashed line (u'/SL, u' - fluctuations velocity, SL - laminar flame speed) which forms the boundary between the wrinkled and corrugated flame sheets. Clearly, if u' < SL and u' is interpreted as the rotation speed of the largest eddies, even these cannot fold the flame. The turbulence merely wrinkles the flame front (see Figure 3.4), and the turbulent burning velocity is largely determined by laminar flame propagation. In spite of the weak influence of the flow field, the average flame thickness will be greater than in the laminar case. The turbulent burning velocity associated with this flame regime can be described by Karlovitz’s result for large scale, low intensity turbulence (which is Damkohler’s equation). In the corrugated flame regime, u'< SL < uK, and the flame front will be pushed around and folded by the largest eddies. The smallest eddies which are just capable of affecting the flame are those with a rotation velocity equal to the laminar burning velocity, and their size is known as the Gibson scale. When Ka = 1, the Gibson scale is equal to the Kolmogorov scale, LG = LK, which means that even the smallest eddies of the flow field are capable of wrinkling the laminar flame surface. The distributed reaction zone regime starts at the line Ka = 1. When Ka approaches unity, and this starts to occur in the wrinkled flame regime, the laminar burning velocity is modified by flame stretch. If Ka = 1, the macro eddies will fold the flame front to form bulges of a size in the order of Lt while the micro scale eddies distort the flame surface into bulges of a size in the the order of LK. If these bulges extend into the unburnt mixture, their radius of curvature is negative, and the local laminar burning velocity becomes less than that of an unstretched flame. At the small bulges the radius of curvature is so small (i.e. the effect of flame quenching due to curvature is so large) that local extinction occurs. The flame is cut into pieces by the small eddies, and these pieces are scattered across the flame zone by the larger eddies. As a consequence there is no well defined flame structure, and the flame front consists of a collection of pockets of unburnt and burnt mixture. In spite of the fact that the laminar flame structure is being disrupted by the turbulence in this combustion regime, the condition Da > 1 indicates that the laminar burning velocity remains a relevant parameter: the local consumption of reactants within a pocket occurs at a rate which is determined by the local laminar burning velocity at its boundary. The overall consumption rate of reactants, however, is determined by the instantaneous interfacial area between the unburnt and burnt mixture. A well known model that is used to describe the average volumetric fuel consumption rate in this combustion regime with success is the so called eddy-breakup model (Spalding, 1971, Bray, 1980). This model relies on the assumption that the overall consumption rate of reactants is determined by the rate at which parcels of unburnt mixture are broken down into smaller ones, thereby increasing the interfacial area between the unburnt and burnt mixture. In the regime of the well stirred reactor, Re > 1, Da < 1 and Ka > 1. The condition Da < 1 indicates that the chemistry is slow in comparison with the turbulence. Under these circumstances the fluid elements of the burning zone are shifted so rapidly in space that no laminar flame structures can be discerned as in the case of the other combustion regimes. The burning zone rather propagates as a homogeneous reactive zone with some reaction occurring everywhere. Spalding D.B. (1971), Mixing and chemical reaction in steady confined turbulent flames. 13th Symposium (Int.) on Combustion, The Combustion Institute, Pittsburgh, 649-657. Gradient and counter-gradient transport in turbulent premixed flamesCounter-gradient transport is the turbulent diffusion of one species against its mean gradient. It can be attributed to the preferential influence of the mean pressure gradient on hot, low-density, burned gases and on cold high-density fresh gases (Kuo 1996). Although both experimental data and theoretical analysis have pointed out the existence of counter-gradient turbulent transport, the practical importance of counter-gradient turbulent transport remains controversial (PoinsotT:2001). Kuo K.K. (1986), Principles of Combustion, A Wiley-Interscience publication, John Wiley and Sons, New York. Content: Fundamentals of hydrogen combustion Non-premixed hydrogen-air combustionLaminar non-premixed flamesTurbulent non-premixed flamesDeflagration basicsEffect of obstacles on flame propagation and pressure build upFlame acceleration which is typically followed an ignition and laminar burning of hydrogen-air mixtures can have different origin. in fact, flame acceleration in all cases is connected with the presence and / or production of turbulence. One can distinguish at least three sources for turbulence production and therefore for flame acceleration:  Figure 1. Accelerating flame (left column), DDT, and quasi-detonation (two right columns) in 2D half-channel with obstacles computed for d/2 = 2 cm, L = 64 cm, dxmin = 1/512 cm. Times in milliseconds are shown in frame corners [Gamezo et al. 2007] The particular process of the flame acceleration is a complex non-linear evolution of pressure perturbations linked to the combustion processes. However, generally it can be considered as a result of interaction of a series of relatively simple events. A flame during its propagation generates acoustic waves that can interact after reflections from the obstacles and channel walls with the flame front and develop flame perturbations through a variety of instability mechanisms. Such instabilities have been observed by Guenoche (1949) and Leyer & Manson (1971) in tubes, by Kogarko & Ryzkor (1992) in spherical chambers, and by van Wingerden & Zeeuwen (1983) and Tamanini & Chaffee (1992) in vented enclosures. Flame acoustic instabilities are usually associated with relatively slow flames in open atmosphere or enclosures that are free of obstacles. Turbulence inducing obstacles have shown to reduce relative contribution of acoustic instabilities on flame propagation and pressure build-up (Tamanini & Chaffee 1992). It has been also shown experimentally that such instabilities can be successfully eliminated by lining the enclosure or tube walls with materials that can absorb acoustic waves (TeodorczykA:1995a). The nature of the acoustic-flame instabilities have been reviewed by Oran & Gardner (1985) and Searby&Rochwerger (1991), Joulin (1994), Jackson et al.(1993) and Kansa&Perlee (1976) studied them in detail. These mechanisms cause flame distortion and wave amplification. Generally, if confinement and/or obstacles are present, several powerful instabilities may strongly influence flame propagation. These are Kelvin-Helmholtz (K-H) shear instability and Rayleigh-Tailor (R-T) density difference instability. In compressible flows the R-T instability is known as Richtmyer-Meshkov (R-M) instability. Both K-H and R-T instabilities are triggered when the flame is accelerated over an obstacle or through a vent. Detailed studies of flame propagation over single obstacle were performed by Wolanski&Wojcicki (1981) and Tsuruda&Hirano (1987). Finally, sufficient fast flames can produce a shock wave that can reflect off a wall and/or an obstacle and interact with the flame. As shown by Markstein&Somers (1953), Scarinci et al.(1993) and Thomas et al.(1997) this can result in severe flame distorsion and in extreme cases cause DDT. Gamezo et al.(2007) have studied flame acceleration in channels with obstacles using advanced 2D and 3D reactive Navier-Stokes numerical simulations. Computations have shown that during flame acceleration shock-flame interactions, R-T, R-M and K-H instabilities, and flame-vortex interactions in obstacle wakes are responsible for the increase of the flame surface area, the energy-release rate, and, eventually, the shock strength. As the flame passes obstacles (Fig. 1), it wrinkles due to R-T instability caused by the flow acceleration. The unreacted flow ahead of the flame becomes sonic. Noticeable shocks begin to form ahead of the flame and they reflect from obstacles and side walls, and interact with the flame triggering R-M instabilities. The K-H instabilities develop at the flame surface when a jet of hot burned material passes through a narrow part of the channel and a shear layer forms downstream of the obstacle. The elevated temperature behind shocks also contributes to the increased energy-release rate. Craven A.D. and Greig T.R. (1968) The development of detonation over-pressures in pipelines. IChemE Symposium Series, 25:41-50.(BibTeX) Effect of flow turbulenceLaminar flame propagation is intrinsically unstable. The nature of the flame instabilities is aerodynamic and possibly, dependent on the molecular weight of the fuel and the mixture composition, diffusional-thermal as well (MarksteinGH:1964). Flame instabilities give rise to flame-generated turbulence (SivashinskyGI:1979). In the most high-reactive fuel-oxygen mixtures such as stoichiometric hydrogen-oxygen and acetylene-oxygen these phenomena are the immediate cause of a run-up to detonation ((SokolikAS:1963) and (KogarkoSM:1965)). In relatively less-reactive fuel-air mixtures these phenomena seem to be controlled by the Huyghens principle owing to which waves tend to a plane geometry (KarlovitzB:1951).  Figure 1. Positive feedback triggered by boundary conditions, the basic mechanism of a deflagra-tive gas explosion. A further speed-up of the process is only possible under the appropriate boundary conditions. Rigid boundaries induce a structure in the expansion flow consisting of velocity gradients and turbulent mo-tion. When the flame contacts such a flow structure, the combustion rate is increased in several ways. The flame is stretched in the velocity gradients, thereby increasing its area and effective burning speed. Turbulence does not only speed up the transport processes of heat and species but, above all, turbulence increases the effective flame surface area i.e. the interface between flammable mixture and combustion products where the reaction takes place. Initially, when the turbulence is of low intensity, the eddies only wrinkle the flame surface and increase its effective area and burning speed. The conse-quence is a stronger expansion flow - flow velocities increase. Higher flow velocities go hand in hand with higher turbulence intensity levels. Under the influence of higher turbulence intensities, the flame front gradually looses its original smooth appearance. Its structure changes. Turbulent eddies tend to disintegrate the front leading to higher combustion rates. Higher combustion rates produce stronger expansion flow and higher intensity turbulence etc ... Turbulence generative boundary conditions trigger a positive feedback in the process of flame propagation by which it develops more or less exponentially both in speed and pressure (CCPS, 1994). The basic concept of a gas explosion can be summarised as a flame propagation process in a flamma-ble mixture, which is sped up by interaction with its self-induced expansion flow field. During this development, the process of turbulent mixing between flammable mixture and combustion products largely determines the combustion rate. The combustion front manifests itself as an extended mixing zone in which the internal interface between flammable mixture and combustion products can become very large. Turbulence generative (boundary) conditions are required for the development of high flame speeds and blast in deflagrative gas explosions. Markstein G.H. (1964) Nonsteady flame propagation. Pergamon Press.(BibTeX) Fast deflagrationsThe studies of deflagration in very rough, obstacle-filled tubes have demonstrated that the flame speed in a given combustible mixture can be varied continuously over three orders of magnitude between the slow limit of a laminar flame to the fast limit of a CJ detonation. The steady flame speed is governed by the boundary conditions in the tube: i.e. geometry and obstacle configurations. It should be noted that the so-called steady flame speed is an averaged value in the direction of propagation over a distance at least of the order of several obstacle spacings or tube diameters, whichever is greater. Large fluctuations are observed locally in the highly three-dimensional transient structure of the flame front. For the so-called quasi-detonation regime (i.e. flame speeds between 1200 m/s and the normal C-J value of about 2500 m/s for fuel-oxygen mixtures) the studies by Teodorczyk et al. and Chan have conclusively demonstrated that the mechanism of propagation is due to auto-ignition via shock reflections. These studies show that normal shock reflections from the obstacle, Mach reflection of the diffracted shock on the bottom wall and Mach reflection of the reflected shock from the top wall can lead to auto-ignition. The role of the obstacle is to promote strong shock reflections leading to high local temperatures for auto-ignition. Detonations are initiated from these local "hot spots" but are later destroyed by diffraction quenching around the obstacles themselves. Hence for quasi-detonations, the diffraction around the obstacles destroys the initiated detonation while shock reflections resulting from the interactions of the decoupled shock with the obstacle and the tube will give rise to local hot spots and re-initiation of the detonation. Experimentally, it has also been observed that there exists a fast deflagration regime (flame speeds between 400 m/s to 1200 m/s) in which the shock reflections are observed to be not strong enough to result in auto-ignition. A decoupled shock and reaction zone complex which propagates at an averaged steady speed is observed. The studies by Teodorczyk have shown that in the fast deflagration regime, shock reflections do not lead to auto-ignition as in the case of quasi-detonations. The mechanism for sustaining the fast propagation speed is intense combustion via flame turbulization by
The importance of transverse waves (and their interaction with the flame) was clearly demonstrated since their elimination results in a significant decrease in the combustion intensity (and hence the deflagration speed). The elimination of the transverse waves also greatly delays the onset of transition from the deflagration to the detonation regime indicating that the transverse waves not only provide a mechanism to promote intense combustion via interface instability, but also a feedback mechanism where the energy released can be coupled to the leading shock front. In a one-dimensional flow the feedback must proceed via the pressure waves generated. Near the sound speed these pressure waves no longer provide the transfer of energy to the front. The structure of a turbulent high speed deflagration consists of a series of compression waves in the front followed by a highly turbulent reaction zone. Lee J.H., Knystautas R., Chan C.K. (1984) Proc.Combust.Inst., Vol.20, p.1663 Deflagrations in a system of connected vesselsFast deflagrationsThe studies of deflagration in very rough, obstacle-filled tubes have demonstrated that the flame speed in a given combustible mixture can be varied continuously over three orders of magnitude between the slow limit of a laminar flame to the fast limit of a CJ detonation. The steady flame speed is governed by the boundary conditions in the tube: i.e. geometry and obstacle configurations. It should be noted that the so-called steady flame speed is an averaged value in the direction of propagation over a distance at least of the order of several obstacle spacings or tube diameters, whichever is greater. Large fluctuations are observed locally in the highly three-dimensional transient structure of the flame front. For the so-called quasi-detonation regime (i.e. flame speeds between 1200 m/s and the normal C-J value of about 2500 m/s for fuel-oxygen mixtures) the studies by Teodorczyk et al. and Chan have conclusively demonstrated that the mechanism of propagation is due to auto-ignition via shock reflections. These studies show that normal shock reflections from the obstacle, Mach reflection of the diffracted shock on the bottom wall and Mach reflection of the reflected shock from the top wall can lead to auto-ignition. The role of the obstacle is to promote strong shock reflections leading to high local temperatures for auto-ignition. Detonations are initiated from these local "hot spots" but are later destroyed by diffraction quenching around the obstacles themselves. Hence for quasi-detonations, the diffraction around the obstacles destroys the initiated detonation while shock reflections resulting from the interactions of the decoupled shock with the obstacle and the tube will give rise to local hot spots and re-initiation of the detonation. Experimentally, it has also been observed that there exists a fast deflagration regime (flame speeds between 400 m/s to 1200 m/s) in which the shock reflections are observed to be not strong enough to result in auto-ignition. A decoupled shock and reaction zone complex which propagates at an averaged steady speed is observed. The studies by Teodorczyk have shown that in the fast deflagration regime, shock reflections do not lead to auto-ignition as in the case of quasi-detonations. The mechanism for sustaining the fast propagation speed is intense combustion via flame turbulization by
The importance of transverse waves (and their interaction with the flame) was clearly demonstrated since their elimination results in a significant decrease in the combustion intensity (and hence the deflagration speed). The elimination of the transverse waves also greatly delays the onset of transition from the deflagration to the detonation regime indicating that the transverse waves not only provide a mechanism to promote intense combustion via interface instability, but also a feedback mechanism where the energy released can be coupled to the leading shock front. In a one-dimensional flow the feedback must proceed via the pressure waves generated. Near the sound speed these pressure waves no longer provide the transfer of energy to the front. The structure of a turbulent high speed deflagration consists of a series of compression waves in the front followed by a highly turbulent reaction zone. Lee J.H., Knystautas R., Chan C.K. (1984) Proc.Combust.Inst., Vol.20, p.1663 Non-uniform mixtures deflagrationsDeflagration in open atmosphereAccelerated flame propagationC. Chan, P. Thibault cited by OECD-SOAR „Flame Acceleration and DDT“ (Breitung, 2000) A freely expanding flame is intrinsically unstable. It has been demonstrated, both in laboratory-scale experiments (Wagner, 1982, Moen, 1982, Lee, 1985, Chan, 1981) and large-scale experiments (Hjertager, 1983, Moen, 1982, Van Wingerden, 1986, Cummings, 1987), that obstacles located along the path of an ex-panding flame can cause rapid flame acceleration. Qualitatively, the mechanism for this flame accel-eration is well understood. Thermal expansion of the hot combustion products produces movement in the unburned gas. If obstacles are present, turbulence can be generated in the combustion-induced flow. Turbulence increases the local burning rate by increasing both the flame surface area and the local mass and energy transport. An overall higher burning rate, in turn, produces a higher flow veloc-ity in the unburned gas. This feedback loop results in a continuous acceleration of the propagating flame. Under appropriate conditions, this can lead to transition to detonation. 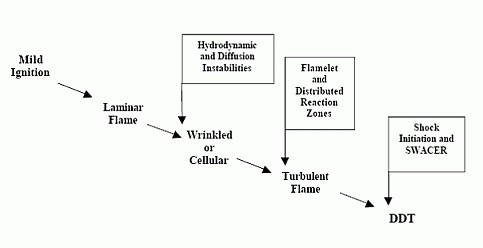 Figure 1. Regimes of flame propagation from laminar flame to deflagration-to-detonation-transition (DDT). Turbulence induced by obstacles in the displacement flow does not always enhance the burning rate. Depending on the mixture sensitivity, high-intensity turbulence can lower the overall burning rate by excessive flame stretching and by rapid mixing of the burned products and the cold unburned mixture. If the temperature of the reaction zone is lowered to a level that can no longer sustain continuous propagation of the flame, a flame can be extinguished locally. The quenching by turbulence becomes more significant as the velocity of the unburned gas increases. For some insensitive mixtures, this can set a limit to the positive feedback mechanism and, in some cases, lead to the total extinction of the flame. Hence, both the rate of flame acceleration and the eventual outcome (maximum flame speed attained) depend on the competing effects of turbulence on combustion. Depending on the fuel concentration and the flow geometry, flame acceleration may be expected to progress through a series of regimes as depicted in Figure 1. For the case of mild ignition, the first phase involves a laminar flame that propagates at a ve-locity determined by the laminar burning velocity and the density ratio across the flame front. This phase of the flame propagation is very well understood and data is available for a wide range of hydrogen-air mixtures. The laminar flame propagation regime is relatively short-lived and is soon replaced by a "wrinkled" flame regime. For most accidental explosions, this regime can persist over relatively large flame propagation distances. For this reason, it is therefore far more important than the initial laminar regime. Due to the increase in flame area, the burning rate, and hence the flame propagation velocity for the wrinkled flame, can be sev-eral times higher than for the laminar flame. 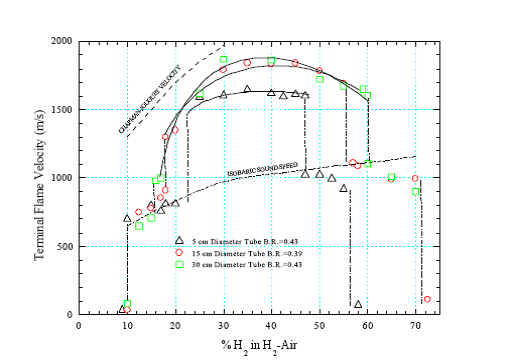 Figure 2. Maximum flame speeds for H2-air mixtures in tubes of different sizes. Due to turbulence generated by obstacles or boundary layers, the wrinkled flame eventually transforms into a turbulent flame brush. This results in further flame acceleration due to the increase in surface area of the laminar flamelets inside the flame brush. For sufficiently high levels of turbulence, the flamelet structure may be destroyed and then replaced by a distrib-uted reaction zone structure. The flame acceleration process can eventually lead to DDT. For configurations involving re-peated obstacles, the turbulent flame propagation regime is self-accelerating due to the feed-back mechanism between the flame velocity and the level of turbulence ahead of the flame front. The final flame velocity produced by the turbulent flame acceleration process depends on a variety of parameters including the mixture composition, the dimensions of the enclo-sure, and the size, shape and distribution of the obstacles. Figure 2 shows the maximum flame speed achievable in tubes of various diameters. Various turbulent flame and detonation propagation regimes have been identified for hydrogen-air mixtures in obstacle-filled tubes. These regimes include: - A quenching regime where the flame fails to propagate;
- A subsonic regime where the flame is travelling at a speed that is slower than the sound speed of the combustion products;
- A choked regime where the flame speed is comparable to the sound speed of the combus-tion products;
- A quasi-detonation regime with a velocity between the sonic and Chapman-Jouguet (C-J) velocity;
- A C-J detonation regime where the propagation velocity is equal to the CJ detonation ve-locity.
It should be noted that the above regimes are geometry-dependent for a given mixture. Con-sequently, the concentration range for each regime in Figure 2 may differ for circular tubes and rectangular channels. Breitung W., Eder A., Chan C.K. e.a. SOAR on flame acceleration and DDT in nuclear safety, O-ECD/NEA/CSNI/R (2000) 7, 2000. Pressure waves from deflagrations: dependence on flame velocity and acceleration Figure 1. Dependence of shock overpressure generated by hydrogen-air deflagration on dimensionless distance for different flame speeds (DorofeevSB:2002). Deflagration processes produce pressure waves ranging from extremely weak acoustic waves, which man can only hear, to extremely strong shock waves in case of detonation, which can produce consid-erable damages. The intensity of pressure wave resulted from deflagration is defined by the intensity of the combustion process. In case of slow subsonic flames the pressure wave typically has gradually growing front with the typical peak overpressure less than 1 bar and duration of several seconds. In case of fast supersonic flames (which are usually fast turbulent flames) the pressure wave transforms into shock (which is characterized by abrupt step-wise changes in media characteristics) with typical overpressures of order of magnitude of 10 bar and its duration of 200 - 500 ms. In the limiting case of detonation a shock wave is also formed but with higher peak values and shorter duration. For example, in case of detona-tion of stoichiometric hydrogen-air mixture at normal conditions an amplitude of detonation wave reaches 17 bar with duration of less than 100 ms. Pressure waves generated by combustion process decay while they propagate from their source. In far zone the amplitude of such pressure wave is defined only by the chemical energy released during com-bustion. This means that for the same amount of hydrogen independently on the intensity and charac-teristics of the combustion process, the overpressure value will be the same. On the other hand (see e.g., Figure 1), in the near zone the observed peak overpressure strongly depends on the speed of combustion. Dorofeev S.B. (2002) Flame acceleration and DDT in gas explosions. Journal de Physique de France IV, 12(7):3-10.(BibTeX) Confined deflagrationsDynamics of flame propagation and pressure build up in closed spaceFlame and pressure dynamics in a closed vessel has been studied best in the simplest case of a spherical vessel with central ignition and spherical flame propagation. At the initial stage of combustion the spherical flame front expands similar to that one in unbounded space – the pressure rise is negligible, vessel walls are relatively far from the flame front to affect the combustion process and the flame front velocity is equal to V_{ff} = s_u E_i , where s_u - burning velocity of the mixture, E_i = \rho _i / \rho _b - expansion coefficient of the combustion products. As the flame propagates closer to the walls the flame front velocity slows down due to compression of the unburnt (fresh) gas. In vicinity of walls the unburnt gas doesn’t expand any more and the flame front velocity equals simply to the burning velocity V_{ff} = s_u . In spite of decelerating flame velocity, the speed of pressure built up is rising owing to the increasing with radius flame front area and, thus, mass burning rate. The most of pressure rise occurs at the final stage of combustion when the flame front is close to the vessel wall. According to the model developed in (DB, Ya. Zeldovich, 1985), for a mixture with expansion coefficient , only 20% of pressure rise occurs during flame propagation over 80% of vessel radius. The pressure during combustion in a closed vessel may be assumed constant across a vessel as the sound speed is much faster than the flame front velocity and pressure equilibration time is much shorter than the combustion time. Combustion process in a closed vessel implies there is no overall gas expansion and the process is accompanied by a pressure rise in a vessel. As the heat of reaction is not spent on work of expansion, but goes solely into raising the internal energy of the gas, the combustion products in a closed vessel have larger temperature compare to combustion of the same fuel-oxidiser composition at a constant pressure. Pressure dynamics with time may be found starting from the balance equation for the burnt mixture mass fraction (Ya.Zeldovich, 1985): m{{d\eta } / {dt}} = \rho \left( {p,\,T_u } \right)\,s_u \left( {p,\,T_u } \right)\,A\left( t \right),
where m - mass of gas in the vessel, \eta - fraction of burnt mixture, t - time, \rho \left( {p,\,T_u } \right) - density of unburnt mixture as a function of pressure P in vessel and temperature of unburnt mixture T_u , s_u \left( {p,\,T_u } \right) - burning velocity, A\left( t \right) - flame area. The flame and pressure dynamics with time may be obtained provided the dependence of the burning velocity with temperature and pressure for a particular mixture and a flame shape are known. Different integral balance models are available from literature, e.g. (BradleyD:1976), (Ya.Zeldovich, 1985), (MolkovVV:1981), (A.Dahoe, 2005). One may use an integral balance model together with inverse problem method to obtain burning velocity of mixture from deflagration pressure dynamics in a closed vessel. Burning velocity and baric index for stoichiometric hydrogen-air deflagration in a large-scale vessel were obtained in (MolkovVV:2000); burning velocity of unstretched hydrogen-air flame was obtained in (A.Dahoe, 2005) in a range of equivalence ratios \Phi = 0.5 - 3.0 from a small-scale closed vessel experiments. More versatile method of modelling flame and pressure dynamics in closed vessels may be computational fluid dynamics (CFD) methods, which don’t require assumption about the shape of a flame front, but, instead, model its development from first principles. For example, a stoichiometric hydrogen-air deflagration in a closed vessel was modelled in (MolkovVV:2004f). There the application of large-eddy simulation (LES) method, which is an advanced method of modelling turbulent and reacting flows, allowed to resolve development of the flame front including the effect of hydrodynamic instabilities. Zeldovich Ya.B., Barenblatt G.I., Librovich V.B., Makhviladze G.M. The mathematical theory of combustion and explosions. Consultants Bureau, New-York, 1985. Mache effectThe temperature gradient exists in the gas burnt in a closed vessel, rising from the gas burnt last to the gas burnt first (B.Lewis, 1961). The temperature gradient is known as “Mache effect” (Ya.Zeldovich, 1985) and was theoretically estimated in a paper (L.Flamm, 1917). In a closed vessel combustion the gas temperature changes due to the heat release and due to adiabatic compression. Generally, an intermediate portion of unburnt gas in a closed vessel may be pre-compressed due to combustion of initial portions of gas, then it burns, producing burnt mixture with a higher temperature, and then these combustion products are compressed again due to combustion of following portions of gas. At initial stage of process (close to ignition point) combustion occurs at initial pressure and temperature and then the combustion products undergo adiabatic compression with corresponding temperature rise. A volume of gas, which burns last, has been pre-compressed initially, and doesn’t undergo future compression and temperature rise after burning. Thus, these gas portions will have different initial conditions, different combustion products temperature and different composition. The Mache effect is known to reduce the explosion pressure below the one for uniform temperature distribution. The Mache effect is strongly pronounced for combustion in a closed spherical vessel with a central ignition, where the gas motion doesn’t cause mixing (Ya.Zeldovich, 1985). Lewis B., von Elbe G. Combustion, Flames and Explosion of Gases. Academic Press, London, 1961. Vented deflagrationsMulti-peaks structure of pressure transients and underlying physical phenomenaVented deflagration pressure dynamics has multi-peak structure. The number of peaks and their magnitude depend on various explosion conditions. Detailed analysis of this peak structure was performed in paper [1]. Vented deflagration of 10% natural gas-air mixture in a vessel of volume V=0.76 m3 with venting area F=V2/3/9.2 and low vent release pressure panel (inertia 3.3 kg/m2) was analysed. Four distinct pressure peaks were registered for the case of vented deflagration in low-strength enclosures (Figure 1).  Fig. 1. Multi-peak structure of vented explosion. The following deflagration phenomena and pressure peak are identified for vented deflagration with initially closed vent cover. After ignition deflagration develops in closed vessel until moment (a) when vent cover is released. So, pressure peak P1 is associated with vent release. At moment (b), when time derivative of pressure is equal to zero, the volume of gases produced by combustion inside the vessel is equal to volume of gases flowing out of the vessel, i.e. \DeltaVdefl=\DeltaVoutflow. It is known that venting of combustion products is more efficient for reducing explosion pressure compared to flammable mixture as for the same pressure drop at the vent a velocity of flow is proportional to square root of temperature. This explains that moment (c) on pressure transient corresponds to the beginning of burnt gas outflow. After it the combustion products “flow through” flammable mixture, which just escaped the vessel, and external explosion occurs at moment (d) with corresponding peak pressure P2. Helmholz oscillations could be generated after external explosion with characteristic wave length longer than resonator (vessel) size. The Helmholz oscillations can induce Rayleigh-Taylor instability [2]. Increase of mass burning rate due to increase of flame front area implies growth of pressure with time. At moment (e) the contact of flame front with walls of the vessel is sufficient for the heat losses to compensate the heat release by combustion and pressure peak P3 is formed. At final stage of the explosion when combustion proceed mainly close to walls and in corners high-frequency oscillations may be generated. Rayleigh criterion is applied in this case: "If heat be given to the air at the moment of greatest condensation, or taken from it at the moment of greatest rarefaction, the vibration is encouraged" [3]. Oscillations of peak P4 can be eliminated by taking adequate measures, such as lining the interior of the vessel to be protected with damping material. It is important to note that when the vent cover failure pressure is increased to 7.5 kPa the second and third peaks practically can no longer be seen on the pressure transient. For relatively high vent release pressures, which are characteristic for process equipment, only two pressure peaks (one - vent release, another - mixture burnout) can be observed. 1.Cooper M.G., Fairweather M., Tite J.P., On the mechanisms of pressure generation in vented explosions, Combustion and Flame, 1986, Vol. 65, Issue 1, pp.1-14. Turbulence generated by venting processFor gaseous explosions the venting process itself is known to cause the flame to accelerate [1]. Gov-erning equations for turbulent vented gaseous deflagrations were derived from the first principles in paper [2]. The inverse problem method for vented gaseous deflagrations has been developed [3] and efficiently used over the years of research allowing to gather unique data on venting generated turbu-lence. For example, an analogue to the Le Chatelier-Brown principle for vented gaseous deflagrations [3] was revealed by this method. The universal correlation for vented deflagrations was developed for the first time in 1995 [4] followed by the closure of this fundamentally new vent sizing approach with the correlation for venting generated turbulence, presented for the first time two years later in 1997 [5]. Two of our previous articles were devoted to the problem of inertial vent covers in explosion protection [6-7]. Recently our original correlations for vent sizing were developed further to include experimental data on fast burning mixtures, such as near stoichiometric and rich hydrogen-air mixtures, and test data on elevated initial pressures [8-11]. The attempts to produce any reasonable correlations for venting generated turbulence have failed for another reason as well – due to a neglect of the role of the generalised discharge coefficient, \mu, which is dependent on vented deflagration conditions. This fact of discharge coefficient dependence on con-ditions was recognised already about 20 years ago by various authors, e.g. [12]. It has been demon-strated in a series of studies that reduced explosion pressure correlates with the deflagration-outflow interaction (DOI) number, that is the ratio of the turbulence factor, \chi, to the discharge coefficient, \mu, rather than with the turbulence factor alone. The following correlation for venting generated turbulence has been obtained by processing a wide range of experimental data on vented gaseous deflagration [11, 13] \chi / \mu = \alpha {\left[ \frac(1 + 10V{_{\#}}{^{1/3}} )(1 + 0.5 Br{^{\beta}}) {1 + \pi{_{\nu}} } \right]}^{0.4} \pi{_{i\#}}^{0.6} where the empirical coefficients \alpha and \beta are equal for hydrogen-air mixtures to \alpha=1.00 and \beta=0.8 and for hydrocarbon-air mixtures to \alpha=1.75 and \beta=0.5; V_\# - dimensionless volume (numerically equal to enclosure volume in m3), V{_\#} = V / V{_{1 m^3}} ; \pi{_{i\#}} - dimensionless initial pressure, ; \pi{_{\nu}} - dimensionless vent closure release pressure, \pi{_{\nu}} = P{_\nu} / P{_i} = (P{_{stat}} / P{_i} + 1) with P_\nu - vent closure release pressure, bar abs., P_{stat} - vent closure release pressure used in the NFPA 68, bar gauge, and P_i - initial pressure, bar abs.; and the Bradley number is Br = \frac {F} {V^{2/3}} \frac {c_{ui}} {S_{ui} (E{_i} - 1)} , where F – vent area, m2; V – enclosure volume, m3; c_{ui} – speed of sound, m/s; S_{ui} – burning velocity at initial conditions, m/s; Ei – combustion products expansion coefficient. The empirical correlation for the DOI number gives the dependence of turbulence level as enclosure scale in power 0.4. This is in agreement with conclusions of fractal theory with corresponding fractal dimension 2.4 for turbulent premixed flame characteristic for vented deflagrations. The turbulent combustion intensifies with increase of the Bradley number as follows from the correla-tion. It means that an increase of venting area F will be accompanied by an increase of turbulence factor. The increase of burning velocity has opposite effect, i.e. a growth of laminar burning velocity will decrease turbulent factor at other conditions being conserved. The DOI number is increasing with increase of initial pressure in enclosure. The turbulence level for vented deflagration in conditions of experiments [14] increased from 4-6 at initial atmospheric pres-sure to 15-20 at initial pressure 7 atmospheres. Hence the increase of initial pressure from 1 to 7 at-mospheres leads to about four-fold increase of the turbulence level. It has been found that there is only 20% increase of the turbulence factor for the stage of deflagration in closed vessel for the same in-crease of initial pressure [13]. This result demonstrates explicitly that it is venting that is responsible for a substantial increase in the turbulence level, but not just an elevated initial pressure itself. 1. Tamanini, F., 1996, Modelling of panel inertia effects in vented dust explosions, Process safety Progress, 15: 247-257. Coherent deflagrations in a system enclosure-atmosphere and the role of external explosionsApparently, Swedish scientists were the first to undertake an experimental investigation in 1957 that emphasised the importance of the external explosion during a vented deflagration [1]. They found that in some cases the maximum explosion overpressure outside a 203 m3 enclosure exceeded the maxi-mum overpressure inside of the enclosure. In 1980 Solberg et al further highlighted the danger of ex-ternal explosions [2]. They found that during vented deflagrations in a 35-mm3 vessel, the flame front propagation velocity could reach 100 m/s in a lateral direction outside the vent. In their experiments the flame propagated up to 30 m outside the enclosure though the vessel was only 4 m long. Harrison and Eyre [3] came to conclusion that for “large vents, where the internally generated pressures are low, the external explosion can be the dominating influence on the internal pressure” and that this influence “could be very important for large volume, low strength structures such as buildings or off-shore modules”. In 1987 Harrison and Eyre [3], and Swift and Epstein [4], independently suggested that the mechanism of external explosion influence on the internal pressure dynamics is contained in the decrease of the mass flow rate through the vent. Theoretical analysis performed by Molkov in 1997 [5], based on the processing of experimental data by Harrison and Eyre [3] confirmed that the turbulence factor inside the enclosure was practically unaffected by the occurrence of the external explosion. Instead, a substantial decrease of the generalised discharge coefficient, i.e. mass outflow, was found for tests with pronounced external combustion. It was concluded that the decrease of the pressure drop on the vent due to combustion outside the enclosure was the main reason for reduced venting of gas outside the enclosure. In 1991 Catlin [6] studied the scaling of external explosions. He found that the external overpressure grows proportionally to the velocity of the flow and flame emerging from the vent. The physics of the phenomenon of coherent deflagrations, i.e. coupled internal and external explo-sions, has been recently clarified [7-9] through application of the large eddy simulation (LES) model developed at the University of Ulster to experiments in 547 mm3 SOLVEX facility [10]. The comparison between experimental and LES pressure transients inside and outside the enclosure and external flame shape led to some important conclusions on the nature of coherent deflagrations. The formation of the turbulent starting vortex in the flammable mixture pushed out of the enclosure during the internal deflagration is a prerequisite for a subsequent intense combustion outside the enclosure. The rapid acceleration of combustion outside the enclosure commences not at the moment when the flame front emerges from the vent, but after the flame front “touches” the edges of the vent. At this point the flame reaches the region of strong turbulence generated in the shear layers at the perimeter of the external jet. There is consequently a rapid increase in the rate of combustion and a coherent steep pressure rise is observed both inside and outside the enclosure. The external pressure rise in the atmosphere is a direct consequence of the highly turbulent deflagration there, but there is no increase of the burning rate inside the enclosure. The pressure rise inside the enclosure is caused by the decrease of mass flow rate from the enclosure to the atmosphere due to the high pressure just outside the vent. In such scenarios the mitigation strategy should aim primarily at the suppression of combustion outside the enclosure. 1. Report of Committee for Explosion Testing, Stockholm, 1957, Kommitten for Explosions Forsok,
Bromma 1957, Slutrapport, Stockholm, April 1958. Le Chatelier-Brown principle analogue for vented deflagrationsThe following relationship could be extracted from a conservative form of the universal correlation for vented gaseous deflagrations [1] and will be used to discuss the Le Chatelier-Brown principle analogue for vented gaseous deflagrations [2] \pi_{red} \sim \left[ S_{ui} \frac{\chi}{\mu} \frac{1}{F} \right]^{25} where \pi_{red} – reduced explosion pressure; S_{ui} – burning velocity, m/s; \chi – turbulence factor; \mu – generalized discharge coefficient; F – vent area, m2. The Le Chatelier-Brown principle analogue states that gasdynamics of premixed turbulent combustion in vented vessel responds to external changes in the process conditions in such a way as to weaken the effect of external influence. Response action is always weaker than primary one. Let us say one would like to reduce explosion pressure \pi_{red} simply through an increase of the venting area F. However, an increase of the vent area F is always (!) accompanied by increase of deflagration-outflow-interaction number \chi/\mu. For example, in experiments on hydrogen-air deflagration [3] 1.5 increase of F is accompanied by 1.25 increase of \chi/\mu. In experiments on 10-20% hydrogen-air defla-grations in spherical vessel of 2.3-m diameter [4] ninefold growth of vent area F was accompanied by 2.79 increase of \chi/\mu for 10% hydrogen-air and 2.93 increase for 20% hydrogen-air mixture. Thus effective increase of venting area for this case is about 3 rather than 9. The same manifestation of the Le Chatelier-Brown principle analogue was observed for hydrocarbon-air mixtures. For propane-air deflagration [3] twofold increase of F is accompanied by 1.57 times increase of \chi/\mu. In experiments by Harrison and Eyre in 30.4 m3 vessel with natural gas-air mixture 2.06 times increase in F was practi-cally compensated by 1.87 increase of \chi/\mu. As a result an effective increase of vent area, i.e. F/(\chi/\mu) is often much less than expected. In the last case the effective increase of vent area is just 2.06/1.87=1.1 (10% only), but not as much as 2.06. Sixfold increase of initial burning velocity Sui, when hydrogen concentration in air increased from 10% to 20% [4], is accompanied by slight, but nevertheless 1.15 decrease of urbulence factor \chi. The significant decrease of the discharge coefficient \mu at the same series of experiments on vented hydrogen-air deflagrations [4] in 2.25 times, when vent diameter changed from 15 to 45 cm due to duct effect, is accompanied by 1.12 decrease of the turbulence factor \chi. Another demonstration of this principle: 1.5 times increase of the turbulence factor \chi in FM Global experiments [5] was compensated partially by 1.25 increase of the discharge coefficient \mu. The Le Chatelier-Brown principle analogue explains why, for example, an increase of venting area is not always so efficient in engineering practice to mitigate explosions to safe level as expected. 1. Molkov V.V., Accidental gaseous deflagrations: modelling, scaling and mitigation, Journal de Physique IV, 2002, Vol.12, pp.7-19 – 7-30. Venting of hydrogen deflagrations through ducts Figure 1. Explosion vessel with vent duct [8]. The discharge of hot combustion products and blast waves from vent devices is often ducted to safe locations to avoid damage to surrounding equipment and buildings. The presence of a duct, however, is likely to increase the severity of an explosion compared to simply vented enclosures. For instance, with stoichiometric acetone-air mixtures it was observed that connecting a duct of 5 cm diameter and a length of 183 cm to a 5 cm diameter vent opening in a 27 liter sphere, increased the reduced pres-sure from 0.7 atm to 4.7 atm [1]. Various authors [2,3,4,5,6] have identified the phenomena that lead to an enhanced explosion severity when a vent device is equipped with a duct: a secondary explosion in the duct due to ‘burn-up’ of reactants emerging from the enclosure, frictional drag, inertia of the gas column in the duct, acoustic interactions, and, Rayleigh-Taylor instability induced by Helmholtz oscillations. The increased explosion severity due to the presence of a duct may be mitigated by three dif-ferent methods: the application of a diaphragm to the vent opening, increasing the discharge pressure, and suppression of combustion in the duct by injecting an extinguishing agent at the onset of the vent-ing process.  Figure 3. Explosion dynamics for a 17% hydrogen-air mixture [8], ignited at the rear location in Figure 1. a) Pressure trace in the explosion vessel. b) Pressure differenceacross the duct entrance. c) Pressure in the initial sections of the duct. d) Rate of pressure rise in the vessel. 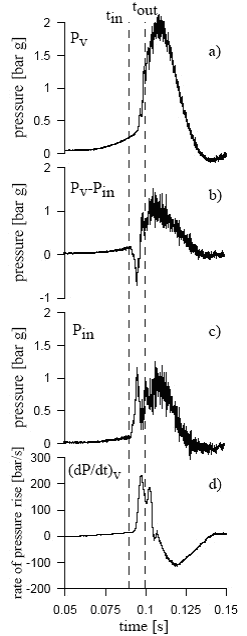 Figure 2. Explosion dynamics for a 4% propane-air mixture [8], ignited at the rear location in Figure 1. a) Pressure trace in the explosion vessel. b) Pressure difference across the duct entrance. c) Pressure in the initial sections of the duct. d) Rate of pressure rise in the vessel. An interesting study of the venting of hydrocarbon-air (methane and propane) and hydrogen-air defla-grations through ducts is described in ref. [8]. These authors investigated the pressure development in a 200-litre cylindrical vessel (length: 1.0m, diameter: 0.5m, see Figure 1). A vent pipe (length: 1.0m, diameter: 0.162m) was fitted to the explosion vessel. The behaviour of the pressure in the explosion vessel and the vent duct is shown in Figures 2 and 3. It is seen that, while the pressure in the explosion vessel with propane-air mixtures remains in the deflagration mode during the ‘burn-up’ in the vent duct, hydrogen-air mixtures exhibit a sudden detonation-like spike. This happens well after the flame has passed the vessel-duct assembly. This phenomenon has been ascribed to the effect of flow reversal across the vessel-duct assembly due to the secondary explosion, and the consequential enhancement of the burning rate of remaining reactants in the explosion vessel. 1. Nekrasov, V.P., Meshman, L.M., and Molkov, V.V., The Influence of Exhaust Ducts on Reduced Explosion Pressure, Loss Prevention in Industry, 5:38-39, 1983 (in Russian). Venting of hydrogen deflagrations with inertial vent covers, jet effectExisting standards, e.g. NFPA 68, address mainly the issue of vent sizing for non-inertial vent covers. However, in various applications only heavy inertial vent closures can be used for technological rea-sons. Most buildings will suffer appreciable structural damage from an internal pressure less than 7 kPa [1]. Deflagration of a hydrogen-air mixture in only 1-2% of an enclosure volume would cause substantial damage. Recent gaseous explosions in domestic structures have shown that new products, such as double glassed windows, can increase the severity of the explosion consequences, up to demolition of most of the building. Most vented deflagrations can be characterised by two pressure peaks. Previous studies have demon-strated that the inertia of the vent cover does influence the value of the first peak, but does not practi-cally influence the second. However, this may not be always the case. An inertial vent cover can affect the second pressure peak in some “implicit” ways. For example, it could happen because of changes in venting generated turbulence, e.g. decrease of turbulence by the gradual opening of the venting area by use of an inertial device. It has been proven that inertial vent covers decrease the maximum turbulence generated during venting, by 20% on average, and by 55% in some experiments with hydrocarbon-air mixtures. This effect could be even more essential for more “sensitive” hydrogen-air mixtures (ex-perimental data are absent at the moment). From another point of view an increase of turbulence could be caused by an increase of vent cover deployment pressure. Indeed, a stronger initial rarefaction wave and consequent pressure oscillations could have a larger effect on the development of flame front wrinkling and hence increase of the burning rate. As another example, it could happen because of changes in the development of “external” explosion during deployment of the inertial vent cover. The jetting of a high-speed flammable mixture into the atmosphere by significantly narrower streams in case of inertial cover deployment contributes to a consequently stronger mixture dilution by air during outflow. This definitely mitigates the external deflagration or could halt it altogether for lean or stoichiometric mixtures of hydrogen with air. Besides, external combustion decreases the pressure drop at the vent and thereby reduces the venting discharge from the enclosure. This in turn causes a higher pressure build up inside the enclosure. Characteristic experimental and simulated (CYNDY code of the University of Ulster) results are pre-sented in the figures below. Figure 1 shows a comparison between theory and experiment [2] for trans-lating vent covers with initially quiescent (test 3-A with a surface density of the vent cover of w=89 kg/m2) and initially agitated by fan (test 3-C, w=42 kg/m2) methane-air mixtures in a 50-m3 enclosure with one 2.45-m2 vent. Two displacement curves for test 3-A are related to two different edges of the vent cover in this particular experiment. The simulated transients are very close to experimental except for the pressure at the final stages of deflagration when the heat losses to the walls reduce the experi-mental pressure.   
Results for experiments with “butterfly” style hinged vent covers [2] are presented in Fig.2 for a 50-m3 enclosure with two 0.957-m2 vents. The comparison with experiments was performed for quiescent (test 3-B, surface density of w=124 kg/m2) and initially turbulent (3-D, w=73 kg/m2) mixtures.   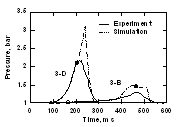
A comparison between theory and experiment (pentane-air) with a spring-loaded vent cover [3] is shown in Fig.3, which refers to the case of a 1.72-m3 enclosure with a 0.164-m2 vent. The mixture was initially quiescent. The surface density of the vent cover was 245 kg/m2. The stepped change of the turbulence factor at the start of vent cover opening can be explained by the high pressure of vent cover deployment (1.55 bar). 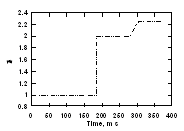 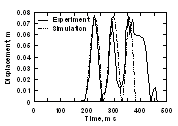 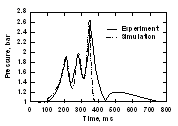
The maximum value of the turbulence factor at the end of the period of its gradual growth in experi-ments with initially turbulent hydrocarbon-mixtures is 70-80% higher than the maximum value for initially quiescent mixtures. It is notable that this difference is larger than the 25-50% initial difference in turbulence factor values due to fan agitation. For the investigated configurations, hinged vent covers result in lower levels of venting generated turbulence than translating vent covers. Vent cover jet effect. This phenomenon was unknown until recently. It significantly affects explosion dynamics in enclosure with inertial vent covers. Several phenomena affecting inertial vent cover dis-placement were examined. The results of the analysis of the drag effect and the air cushioning effect between the moving vent cover and its constraints suggested that these two phenomena were insuffi-cient to account for the experimentally observed displacement of the vent cover. It has been demon-strated that the formation of a jet of flowing out of an enclosure gases on an “internal” surface of the inertial vent cover drastically influences the movement of the cover and hence affects the transient explosion pressure. Mathematical modelling of the pressure distribution, including the jetting flow of explosion products, resulted in a pressure force on the vent cover half that predicted by traditional modelling for translating covers. It was determined by comparison with experiments that the change from full to reduced pressure due to this jet effect becomes significant when the virtual venting area reaches 5-10% of the nominal venting area. The jet effect is crucial to simulating explosion dynamics for all types of venting devices: moving in translation, rotation or spring-loaded [4-7]. References 15. Howard W.B., Karabinis A.H., Tests of explosion venting of buildings, Plant/Operations Progress, 1982, Vol.1, No.1, pp.51-65. DDT basicsPhenomenology of flame acceleration and deflagration to detonation transitionThe sequence of events leading to detonation in a tube containing explosive gases can be summarized as follows:
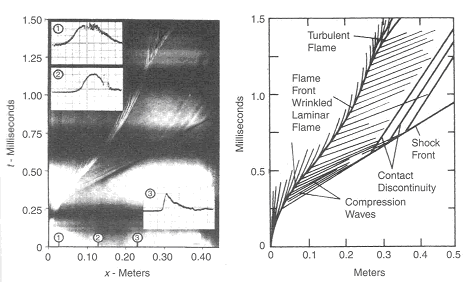 Figure 1a. The development of detonation in stoichiometric H2-O2 mixture initially at normal temperature and pressure, showing the generation of pressure waves ahead of the accelerating flame. 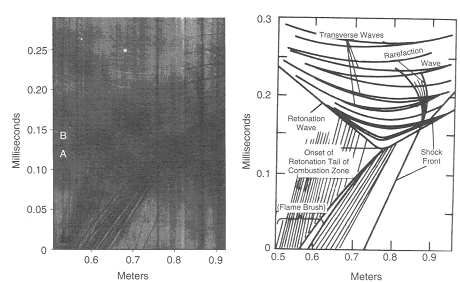 Figure 1b. The onset of retonation. For both photographs spark ignition by discharging 1.0 mJ. Electrodes located at closed end of 25 x 37 mm cross-section tube (Oppenheim et al., 1963). Streak schlieren photographs. The forward-mowing wave was studied using wall imprints of the detonation process, an example of which is shown in Fig. 3. The characteristic fish-scale pattern, which corresponds to inception of the forward shock, is a distinguished feature of a self-sustained detonation front. There are generally four different modes of transition process observed and classified, based on the location of the onset of an “explosion in an explosion”: between flame and shock front (Fig.4a), at the flame front (Fig.4b), at shock front (Fig.4c) and at the contact discontinuity (Fig.4d). The oset of detonation depends on the particular pattern of shock fronts created by the accelerating flame. The process of DDT is unreproducible in its detailed sequence of events. DDT refers to the phenomena where the critical conditions for the onset of detonation are established by the combustion process itself without external energy source. There are several ways by which the conditions necessary for transition can be achieved. These include:
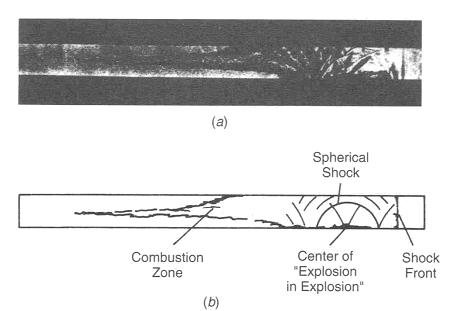 Figure 2. Flash schlieren photograph of the onset of retonation in a stoichiometric H2-O2 mixture initially at normal temperature and pressure at an instant marked by A on streak schlieren photo (Fig.1)(Oppenheim et al., 1963).  Figure 3. Wall imprints of the transition process.  Figure 4. Various modes of DDT observed in 2H2+O2 mixture; a) onset occurring between flame and shock, b) onset occurring at flame front, c) onset occurring at shock front, d) onset occurring at contact discontinuity. (Urtiew and Oppenheim, 1966). Effect of chemical composition, pressure, temperature, geometry, and system physical scaleEffect of non-uniformity (SWACER) In DDT process energy required to initiate detonation is provided by rapid release of energy during combustion to produce a blast wave of sufficient strength to cause detonation. As described by Lee (LeeJHS:1980), such shock waves can be produced by prescribing a spatial and temporal coherence of the energy release. Theoretically, the required coherence can be achieved by pre-conditioning the explosive mixture so that the induction time \tau increases in a prescribed manner away from an initial ignition point to produce energy source which propagates at a velocity V_0 = (\partial \tau /\partial x)^{-1} . Spatial gradients in induction time are due to gradients in temperature and/or free radical concentrations. The so-called SWACER (Shock Wave Amplification by the Coherent Energy Release) mechanism was first proposed to account for photochemical initiation in H2-Cl2 mixtures. Gradients in temperature and free radicals are also produced by turbulent mixing of hot combustion products with unburned gas in turbulent eddies associated with flame propagation around obstacles or in turbulent flame jets. Knystautas et al. (KnystautasR:1979) achieved DDT by injecting a hot turbulent jet into a quiescent fuel-oxygen mixture. Coherent energy release by itself is not enough for DDT, the volume of coherent energy release must be also be large enough to produce a strong enough shock wave with long enough duration to initiate detonation in the surrounding unburned mixture. A lower bound of the volume required for transition to occur in an unconfined cloud can be obtained by equating the chemical energy in a spherical volume to the critical initiation energy by an external source: E_{c} =\frac{\pi \rho _{0} QD_{c}^{3} }{6}
where Q is the chemical energy release per unit volume, \rho_0 is the density of the unburned mixture, and D_c is the critical explosion diameter. Lee J.H.S. and Moen I. O. (1980) The mechanism of transition from deflagration to detonation in vapor cloud explosions. Progress in Energy Combustion Science, 6:359-389.(BibTeX) Criteria for spontaneous flame acceleration to supersonic flame speed Figure 1. Observed combustion regime as a function of expansion ratio \sigma and dimension- less activation energy Ea/RTu for hydrogen-air and hydrocarbon-air mixtures for closed systems. Picture reproduced with permission from (DorofeevSB:2001). The next phenomenon which strongly influences the route of combustion process is flame acceleration. As it was shown in (DorofeevSB:2001), the possibility of flame acceleration is defined by mixture properties. The experimental data on the combustions in confined volumes from a wide variety of test facilities with the different characteristic lengths and the geometric configurations were analyzed. The analysis showed that strong flame acceleration was observed only for the sufficiently sensitive mixtures (Figure 1). The parameter, which controls the possibility of flame acceleration, was identified as an expansion ratio \sigma (ratio between density of unburned and burned mixture at constant pressure). An expression of critical expansion ratio (below which the flame acceleration is not observed) reads as \sigma^* = 0.9 \times 10^{-5} \cdot x^3 - 0.0019 \cdot x^2 + 0.1807 \cdot x + 0.2314, \ \ \ \ \ (1)
where x is dimensionless activation energy x = Ea/RTu . For hydrogen-air mixtures this parameter is approximately equal to 25 and, therefore, for critical value \sigma^* gives approximately value of 3.7. In case of systems with partial transverse venting (as it was shown in [4], see Figure 2) the critical value \sigma^* is modified proportionally to vent ratio \alpha (ratio between surface of vent and surface of enclosure). The larger is the vent area the more reactive mixtures is necessary for development of fast flames. The resulting expression for critical expansion ratio reads as \sigma_{cr} = \sigma^* \cdot (1 + 2.24 \cdot \alpha)
where \sigma^* is critical expansion ratio for closed systems (Eq. (1)). On the basis of findings of [(DorofeevSB:2001), (AlekseevVI:2001)], it is possible to formulate a criterion for strong flame acceleration: the mixture can exhibit strong flame acceleration only if its expansion ratio is larger than critical expansion ratio \sigma^{cr} . This statement has to be supplemented with the following: strong flame acceleration can take place only if there is enough room for actual development of supersonic flame. This geometric limitation is connected with necessity of run-up distance for flame acceleration process, which can be evaluated for tube-like configurations as having value of 20-40 diameters (see, e.g., [5]). Such formulated criterion has a character of necessary condition and thus can be directly used for evaluation of flame acceleration potential in CFD simulations. 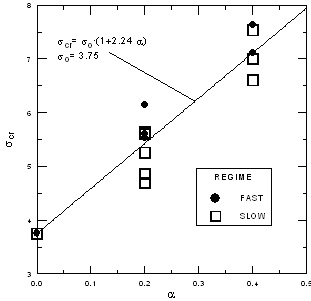 Figure 2. Observed combustion regime as a function of expansion ration \sigma and vent ratio\alpha . Dependence of critical expansion ratio \sigma^{cr} on \alpha . Picture reproduced with permission from (AlekseevVI:2001). Note, that the proposed criterion has, unfortunately, only limited range of applicability, since it was deduced on the basis of data obtained in confined and confined with partial venting systems. The generalization of this criterion to lower degrees of confinement and to open systems should provide extremely useful information for evaluation of flame acceleration potential in safety analysis. Dorofeev S.B., Kuznetsov M.S., Alekseev V.I., Efimenko A.A. and Breitung W. (2001) Evaluation of limits for effective flame acceleration in hydrogen mixtures. Journal of Loss Prevention in the Processes Industries, 14:583-589.(BibTeX) Criteria for establishment of stable detonationOne of the most important critical event, which can strongly affect the regime of combustion, is deflagration-to-detonation transition. For many years many efforts was being made to develop a theory of this event, however it is still far from complete understanding. Due to this fact, the DDT predictions from CFD simulations hardly can have reliable character. To avoid uncertainty in forecast of DDT a criterion for detonation onset was proposed. 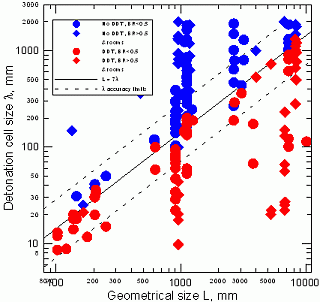 Figure 1. Critical conditions for onset of detonations in rooms and channels with obstacles. Deviations from line L = 7\lambda are within 30%. Picture reproduced with permission from (DorofeevSB:2000). For systematization of conditions in which DDT event can take place, numerous sources of data were analyzed in (DorofeevSB:2000). The literature data and the data from experiments carried out by authors were used. It was shown that depending on geometry of the facility, the mixture of the same composition can exhibit different behavior. In the facilities with characteristic length large than certain value (defined by mixture reactivity) the mixture does detonate, and in smaller facilities the detonation does not occur. The results of analysis are summarized in Figure 1. Solid line L = 7\lambda separate analyzed cases with observed detonation from cases without detonation onset. As it was indicated by authors an accuracy of such separation is within 30% of \lambda value. Parameter \lambda, which is used as characteristic length for characterization of mixture sensitivity, is detonation cell size. Detonation cells are imprint of complex three-dimensional structure of detonation wave and their size is determined by mixture properties only (e.g., H2 concentration, initial temperature) and does not depend on geometric configuration of detonating mixture. The values of detonation cells are often known only with inaccuracy of 100%, therefore an application of 7\lambda correlation has to be made with understanding of accuracy of this correlation. A criterion built on basis of 7\lambda correlation reads as: for detonation onset to be possible a characteristic size of combustible mixture (cloud or room size) must exceed 7\lambda (necessary condition). If detonation develops as a transition from fast deflagration, the corresponding criterion for flame accelleration has to be fulfilled as well. Note that this criterion as well as criterion for flame acceleration has limited character of applicability since for non-uniform mixtures with spatially dependent properties (e.g., concentration) assessments of detonation cell size and expansion ratio can have considerable uncertainties in their values. However, by the moment these criteria provide the most reliable methodic on the potential of flame acceleration and DDT events. Dorofeev S.B., Sidorov V.P., Kuznetsov M.S., Matsukov I.D. and Alekseev V.I. (2000) Effect of scale on the onset of detonations. Shock Waves, 10:137-149.(BibTeX) Transition to detonation during venting of hydrogen deflagrationsSWACER mechanismDetonation basicsDetonation direct initiationDirect initiation of detonation can be achieved by condensed explosives, explosion of another gas mixture, electrical wire explosion, high-voltage sparks, and laser sparks. The conditions are characterized by the critical (minimal) energy E^*_n required to produce a shock wave going over to a self-sustained detonation; n = 1, 2, 3 denotes planar, cylindrical, and spherical waves respectively. The rapid release of a spatially concentrated source of energy results in the production of a decaying blast wave in the surrounding gas. A very strong gradient in temperature and pressure occurs behind the blast wave and serves to quench the chemical reaction. On the other hand, the very high temperatures produced behind the blast induce very rapid chemical reaction. The net effect of quenching due to strong gradient and accelerated reaction due to strong blast waves result in either initiation or failure depending on the strength of the source. A heuristic limiting condition proposed by Zel'dovich (ZeldovichYaB:1956) is that at least one reaction time must have elapsed before the instantaneous Mach number reaches the CJ value for initiation to be successful. Combining this simple criterion with strong blast wave (similarity) theory results in a quantitative prediction for the critical energy (LeeJHS:1966). In a spherical geometry, the result is: E_{c} =I\left(\gamma \right)\rho _{0} D_{CJ} \Delta ^{3},
where \Delta is the induction length and I\left(\gamma \right) is a constant of the order of 1 determined by blast wave theory. This expression can be used together with detailed kinetic computations of the reaction zone length to estimate the critical initiation energy for specific fuel-oxidizer mixtures. Atkinson (AtkinsonR:1980) showed satisfactory agreement between their kinetic computations and experimental data for hydrogen-air initiation. Zeldovich Ya.B., Kogarko S.M. and Simonov N.N. (1956) An experimental investigation of spherical detonation of gases. Soviet Physics - Technical Physics, 1:1689-1713.(BibTeX) Hugoniot curveFor steady, one-dimensional flow of a combustible gas that burns to completion, equations relating initial and final conditions are called the Rankine-Hugoniot relations and they provide jump conditions across the front, from upstream (subscript 0) to downstream (subscript \infty ) . These equations are: 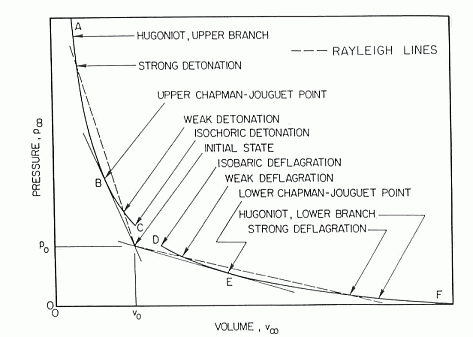 Figure 1. Schematic locus of burnt-gas states for combustion waves (LinanA:1993). m_{0} \equiv \rho _{0} u_{0} =\rho _{\infty } u_{\infty } P_{0} \equiv \rho _{0} u_{0}^{2} +p_{0} =\rho _{\infty } u_{\infty }^{2} +p_{\infty } The sequence of final states obeying p_{\infty } +m_{0}^{2} /\rho _{\infty } =P_{0} \equiv p_{0} +m_{0}^{2} /\rho _{0} obtained by substituting first two equations, is the Rayleigh line, a straight line in the plane of final pressure p_{\infty } , and specific volume, 1/\rho _{\infty } , such as Fig.1. Use of energy conservation equation together with second jump condition provides a relationship among thermodynamic properties, the Hugoniot curve, which can be written as: \left(\frac{\gamma }{\gamma -1} \right)\left(\frac{p_{\infty } }{\rho _{\infty } } -\frac{p_{0} }{\rho _{0} } \right)-\frac{1}{2} \left(\frac{1}{\rho _{\infty } } +\frac{1}{\rho _{0} } \right)\left(p_{\infty } -p_{0} \right)=h_{0} where h_{0} is the total amount of chemical heat release per unit mass of the mixture, The Hugoniot curve is shown schematically in Fig. 1 for a representative combustion system. The final state is determined by the intersection of the Rayleigh line with the Hugoniot curve. The Hugoniot curve has two branches, an upper branch of large \rho _{\infty } and p_{\infty } , called the detonation branch, and a lower branch of small \rho _{\infty } and p_{\infty } , called the deflagration branch. There is a minimum propagation velocity for detonations, corresponding to tangency at the upper Chapman-Jouget point. The Rankine-Hugoniot equations can be solved by e.g., STANJAN code, examples of results from such computations for hydrogen-oxygen and hydrogen-air mixtures are given in Table 1. Table 1. Calculated detonation properties for hydrogen mixtures with oxygen and air initially at 298 K and 1 atm (ReynoldsWC:1986).
Overdriven detonationUnder certain circumstances, it is possible for the detonation wave to move faster than the unique steady-state velocity given by CJ theory. This usually occurs because another event causes the detonation products to move faster than the velocity they would have in a CJ wave. As a result, the pressure associated with the overdriven detonation front can be significantly higher. The extent of pressure increases that can occur can be seen in Table 2 for hydrogen-air and hydrogen-oxygen detonations. Table 2. Theoretical pressure (bar) for overdriven detonation in stoichiometric hydrogen mixtures (TeodorczykA:1992).
Linan A. and Williams F.A. (1993) Fundamental Aspects of Combustion. Oxford University Press.(BibTeX) Chapman-Jouget detonationOne-dimensional detonation theory was developed independently by Chapman (ChapmanDL:1899) and Jouguet (JougetE:1906) and was based on the preceding shock theory, with the inclusion of an addition energy term corresponding to the energy released by chemical reaction. In this theory, the C-J theory, the chemical reaction is assumed to occur infinitely fast. Further manipulation of equations leads to the following expression q_{CJ} =\frac{\left(M_{CJ}^{2} -1\right)^{2} a_{1}^{2} }{2\left(\gamma _{b} -1\right)M_{CJ}^{2} \left(\gamma _{b} +1\right)},
which relates the resulting wave Mach number M_{CJ}, the corresponding energy release q_{CJ}, the sound speed in the initial reactants a_{1} and the ratio of specific heats of the product gases \gamma_{b}. In a CJ detonation, the reactants at an initial pressure, temperature and density are transformed instantaneously to products at a final pressure, temperature and density. The CJ theory gives a remarkably accurate prediction of detonation velocities based only on a knowledge of the initial conditions and despite the actual complexity of a real detonation. Chapman D.L. (1899) On the Rate of Explosion in Gases. Physics of Fluids, 47:90-104.(BibTeX) Detonation limitsExperiments show that there exist definite limits beyond which a detonation cannot exist. These depend on the composition, temperature and pressure of the mixture, and also on the geometry and roughness of the vessel. Approaching the detonation limits the detonation wave first begins to pulsate, becomes “multi-headed” and then changes its character completely: the detonation front starts to move along a helical path – this mode is called spinning detonation. Table 1 shows limits of detonability in comparison with deflagration limits which are wider. Detonability limits of confined mixtures are not unique, but strongly depend on the boundary conditions of the medium in which the detonation propagates. This is shown by the results of Table 1 from the experiments performed in tubes of different diameter. Table 1. Experimental deflagration and detonation limits for hydrogen.
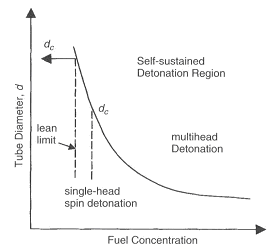 Figure 1. Effects of fuel concentration and tube diameter on the onset of single-head spin detonation (KuoKK:2005) Over the range of detonable concentrations of a given fuel-oxidizer mixture, the wave structure is called multi-head wave front. This wave is characterized by relatively weak transverse waves in compari-son to the axial component, which allows it to be considered roughly one-dimensional as in the ZND model. It has been observed that, in a given smooth circular tube, as the mixture composition becomes leaner or richer, the multi-head, self-sustained detonation becomes a single-head spinning detonation propagating at about the CJ velocity. The critical tube diameter dc for detonation propagation in un-confined space outside the tube was discovered which is related to the characteristic transverse wave spacing (detonation cell size) \lambda by:
A schematic illustration of wave motion in a detonation cell is shown in Figure 1 in article Detonation front structure. In Figure 1 the tube diameter is plotted against fuel concentration around the lean limit. In the region above the curve, known as the self-sustained detonation region, multi-head detonations propagate. As early as (KogarkoSM:1948) proposed that, at the onset of single-head spin in a smooth circular tube, the detonation cell width \lambda , must be equal to the tube circumference, \lambda = \pi d^*
This limiting tube diameter is designated as d*. Later this criterion was confirmed by (LeeJHS:1985) and (DupreG:1985). Figure 2 presents critical tube diameter for hydrogen and some hydrocarbon fuels and Figure 3 shows limiting tube diameter for same fuels.  Figure 2. Correlation of critical tube diameter with the empirical law d_c = 13 \lambda (KuoKK:2005) 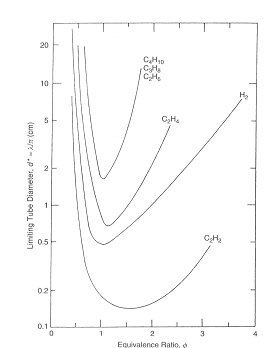 Figure 3. Variation of the minimum limiting tube diameter d^* = \lambda / \pi for stable propagation of detonation in tube Kuo K.K. (2005) Principles of Combustion. John Wiley \& Sons, New York.(BibTeX) Detonation front structureStandard practice of evaluation possible hazards, which can come from detonation precesses is usually based on the theory of steady state one-dimensional detonation. The predictions of such theory are well-known and usually can have sufficient accuracy to provide necessary information for industrial designs. 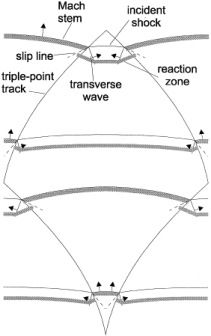 Figure 1. Schematic presentation of multi-dimensional detonation front structure (KuoKK:2005). However there are numerous examples demonstrating non-stationary and multi-dimensional nature structure of the detonations. These features can affect the maximum local pressures during detonation process and therefore can be important from the point of view of safety aspects for industrial applications. Detonation waves in the mixtures, which are far enough from detonation limits, have internal multi-dimensional structures. Already classical works on structure of detonation waves, e.g. ((VoitsekhovskiiBV:1966), (StrehlowRA:1970), (StrehlowRA:1969b), (StrehlowRA:1969c)), permitted to discover different type of detonation waves:
In case of lean or reach mixtures, which are close to their detonation limits, detonations occur usually exhibiting characteristics of the second or third types. Unfortunately, most of the experimental work was performed for the mixtures far from detonation limits, and detonations of marginal mixtures are not studied in full volume. Note that the role of front structure, as a rule, appears to be more significant in case of lean mixtures detonations, which are typical for industrial accidents. Multi-dimensional structure of the detonation front includes leading shock wave and a number of transverse waves, which propagates perpendicular to the leading shock, reflecting from each other and from bounding walls. The surface of the leading shock consists of the sequence of convex parts, which start chemical reaction, and concave parts which are fast decaying waves. Additional reaction zones are located behind the transverse waves where the reaction completes. {bibtexcitelist:AS} Detonation cell size Figure 1. Detonation cells in tests In Figure 1 of the article Detonation front structure a diamond-shaped form demonstrates a typical track of triple points from intersecting shock waves. Such track is called detonation cell and can be easily obtained experimentally on sooted surfaces located in detonating gases. These cells form a cellular structure observed experimentally, and are characterized by their two lengths: longitudinal size L and transverse size S. These two lengths are varying depending on type of burnable gase and initial conditions, how-ever the relation S ≈ 0.6 L are kept usually constant. In Figure 1 an example of detonation cell in stoichiometric hydrogen-air mixture is shown. In the figure a soot track of irregular detonation cellular structure in stoichiometric H2-air mixture is shown (KuznetsovMS:2000), (KuznetsovM:2002c). Average transverse cell size of the test shown in the figure S ≈ 1 cm. The detonation cell size is kept constant for the given components for the same initial condition and depends only on the mixture composition, and therefore is often used as a mesure of mixture reactivity. 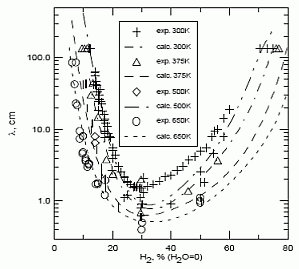 Figure 2. Detonations cell sizes Usually the detonation cell size reaches its minimum at the stoichiometry composition and grows for leaner and richer mixtures. In Figure 2 a dependence of the detonation cell size for H2-air mixtures on initial H2 concentration and mixture temperature ((CiccarelliG:1994) (KaneshigeM:1997) is shown. Kuznetsov M.S., Alekseev V.I. and Dorofeev S.B. (2000) Comparison of critical conditions for DDT in regular and irregular cellular detonation systems. Shock Waves, 10:217-224.(BibTeX) Detonation stabilityGaseous detonations propagating close to the Chapman-Jouguet (CJ) velocity all have unstable fronts, and there is a large body of work (Voitsekhovskii et al. 1966, Strehlow 1964, Oppenheim et al. 1968, Urtiew 1970, Edwards et al. 1972) documenting the common features of oscillations in the main shock strength, weak shocks moving transversely to the main front, and the quasi-periodic or cellular nature of the disturbances. These features are particularly prominent in mixtures with large amounts of monatomic gas dilution. 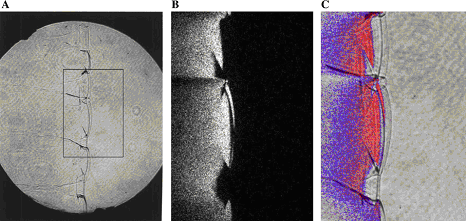 Figure 1. Images of detonation front propagating from left to right in 2H2-O2-12Ar, P1 = 20 kPa in the narrow channel. (A) Schlieren image. The box shows the location of the corresponding OH fluorescence image shown in (B). (C) Super-imposed schlieren and fluorescence images (the false color is a function of the intensity of the signal). PLIF image is 60 mm high. Traditionally, the degree of detonation front instability has been classified by the regularity of the cellular structure as determined from soot foils by visual inspection (Strehlow 1969) and image analyses (Shepherd et al. 1986). As an alternative, one can use the distance from the longitudinal neutral stability boundary in reduced activation energy versus Mach number coordinates as a figure of merit to quantify the degree of instability. For hydrogen mixtures the activation energy is the dominant parameter. In the context of a single-step irreversible reaction rate, detonation waves are stable if the activation energy Ea is less than a critical value, which depends on the ratio of specific heats \gamma , chemical energy content Q/RT1 of the mixture, and overdrive factor f =(U/UCJ)2. Eckett (2000) showed that the one-dimensional neutral stability curve for f = 1 is independent of \gamma if expressed in terms of the reduced activation energy \Theta = Ea/RTvN where TvN is the temperature at the von Neumann state and the CJ Mach number, MCJ. Weakly unstable detonations occur in mixtures with stability parameters (\Theta \approx 5, MCJ \approx 4.6). In particular, this category includes detonations in 2H2-O2 with more than about 50% Ar dilution; these mixtures are well known to have very regular soot foil patterns. An image of weakly unstable detonation is shown in Fig.1. 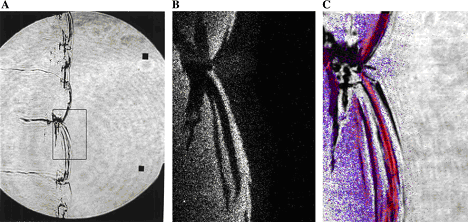 Figure 2. Images of detonation front propagating from left to right in 2H2-O2-3.5N2, P1 = 20 kPa in the narrow channel.(A) Schlieren image. The box shows the location of the corresponding OH fluorescence image shown in (B). (C) Superimposed schlieren and fluorescence images. PLIF image is 30 mm high. N2-diluted 2H2-O2 mixtures with \Theta \approx 7 may be classified as moderately unstable. These mixtures have soot foil patterns that are less regular than those of the weakly unstable mixtures. A sample image of a moderately unstable detonation front is shown in Fig. 2. The mixtures such as H2-N2O-1.33N2 or H2-N2O-1.77N2 with \Theta \approx 11 may be classified as highly unstable. Austin J.M., Pintgen F., Shepherd J.E. (2005) Proc.Comb.Inst. 30, pp.1849-1857 Steady and unsteady detonationsNon-uniform mixtures detonationsThe problem of detonation initiation through transmission of detonations from one explosive mixture to another connects the problem of blast initiation with the problem of spontaneous detonation. The phase of a detonation transmission to a less sensitive mixture plays an important role in the spontaneous initiation of a detonation (Kryuchkov, 1996; Kuznetsov, 1997). Reinitiation of detonation across inert or insensitive gaps and detonation transmission to less sensitive mixtures were studied by Bull (1981), Thomas (1991), Engebretsen (1991) and Teodorczyk (1995).These investigations showed that detonation reinitiation was enhanced by increase of detonation parameters in the donor mixture, decrease of the length of a gap and increase of the reactivity of the acceptor and gap mixtures. It was also found that the critical driver length for detonation transmission increases with decrease of acceptor mixture sensitivity. Ratios of the critical driver length Lc to characteristic chemical length scales, such as detonation cell width \lambda , critical tube diameter dc, and reaction zone width \delta , were found to be functions of effective intensity of initiating wave. The latter depends on both difference in the energy content of the mixtures and their reaction rates. Kryuchkov S.I., Dorofeev S.B., Efimenko A.A. (1996), Critical Conditions for Detonation Propagation Through Mixture with Decreasing Reaction Rate, Proceeding of the Combustion Institute, Vol.26, 2965-2972 Strategies in the prevention of detonation
Laminar diffusion flamesBurke-Schumann flame structure Figure 1. The shapes of laminar diffusion flame under: a) over- and b) underventilated situations [Chomiak 1990] Diffusion flames are when the fuel and oxidizer are physically separate so that the energy release rate is limited primarily by the mixing process. There is no fundamental flame speed as in the case of premixed flames. Chemical kinetics plays a secondary role. Diffusion flames occur with flowing gases, with vaporization of liquid fuels and with devolatilization of solid fuels. It follows from the experimental data that the reaction zone in diffusion flames is thin, just as in premixed flames, and can be treated as flame front. The flame front is located where the stream of the original components flowing into the combustion zone meet in a stoichiometric ratio. A classical example of a laminar diffusion flame, which was first described quantitatively by Burke and Shumann, is provided by a system in which fuel and air flow with the same linear flow velocity in coaxial cylindrical tubes. The observed shapes of diffusion flames may be divided into two classes. If the ratio of the dust radii rs top rj is such that more air is available than what is required for complete combustion, than an overventilated flame is formed and the flame boundary converges to the cylinder axis. On the other hand, if the air supply is insufficient for complete burning, than underventilated flame is produced in which the flame surface expands to the outer tube wall (Figure 1). The flame shapes and flame heights calculated from Burke and Shumann theory are in good agreement with experiments. Figure 2 shows some of the computed profiles and experimental data points. 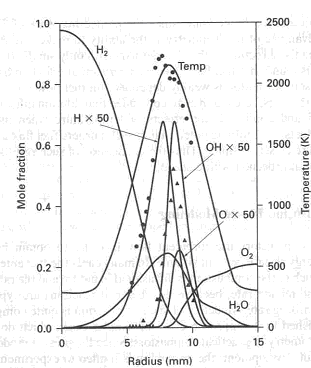 Figure 2. Concentration and temperature profiles in a hydrogen-air diffusion flame at 2 cm above fuel inlet; the hydrogen tube had a 5 cm radius; circles are measured temperatures and triangles are measured OH concentrations [Fukutani et al. 1991] Chomiak J. (1990) Combustion. A Study in Theory, Fact and Application. Gordon and Breach Science Publishers Turbulent diffusion flamesTurbulent diffusion jet flame: flame structure, specific features; scales and combustion regimes in turbulent non-premixed combustionThe diffusion is the rate-controlling process in turbulent diffusion flames. The characteristic time scales for convection and diffusion are normally much larger than the characteristic time scale of the combustion processes. The assumption of infinitely fast chemistry, or local chemical equilibrium, is therefore justified in some cases. This means that the modelling can be significantly simplified. However, there are situations where the assumption of fast chemistry does not hold, i.e. reactions involving CO and NOx, where the finite rate chemistry must somehow be represented. Local quenching, lift-off and blow-off can occur when the local diffusion time scale is of the same order of magnitude as that of the chemical timescale of the reactions. The assumption of local chemical equilibrium makes it possible to predict the flame length of a jet flame. Central to this is the introduction of mixture fraction, a conserved scalar, which is independent of chemistry. All scalars, such as density, temperature, species concentrations, are uniquely related to the mixture fraction. Combustion regimes There are four regimes in non-premixed turbulent combustion
For large mixture fraction fluctuations, Z'_{st} > (\Delta Z)_f , a regime of separated flamelets exists. The reaction is connected when Z'_{st} < (\Delta Z)_f , i.e. when the mixture fraction fluctuation is smaller than or equal to the diffusion thickness in mixture fraction space. Relationship between flame height and fuel flow rateLaminar diffusion flames: L \sim \dot{m}_{fuel}Hottel and Hawthorne (1949) suggested that a hydrogen-fuelled flame would undergo transition from laminar to turbulent flow at a Reynolds number of around 2000. Flame length is defined as the distance between the nozzle exit and the point on the jet centreline whe-re the mean mixture fraction equals the stoichiometric mixture fraction. Axisymmetric jet ejecting vertically upward – \frac{L + x_0} {d} = \frac {5.3} {Z_{st}} \left( \frac{\rho_0}{\rho_{st}} \right)^{1/2},
where x_0 is the virtual origin, d is the jet diameter, Z_{st} is the stoichiometric mixture fraction, \rho_0 is the ambient density and \rho_{st} is the density of a stoichiometric mixture. Peters and Göttgens (1991) presented a relation between a non-dimensionless flame length and the Froude number for buoyant diffusion flames. Peters (2000) included a graph showing the flame length against Froude number for propane-air diffusion flames. Vertical jet ejecting upwards – quiescent ambient conditionsThe flame will be longer if the jet is ejecting vertically upwards and buoyancy is taken into account. Vertical jet ejecting upwards – crosswind ambient conditionsThe momentum of the crosswind will cause the flame to bend over with the wind. Even a crosswind with relatively low momentum would make a high momentum jet bend over. Muppidi and Mahesh (2005) used DNS to simulate high momentum jets in a low momentum cross flow; A jet with a mo-mentum ratio of 1.5, Mjet/Mcrossflow, would be deflected at y/d \lambda 1.5 and a jet with a momentum ratio of 5.7 would be deflected at y/d \lambda 6. The jet will exhibit the characteristic kidney-shape due to counter-rotating vortices, which draws ambient air into the jet. The mechanism responsible for the formation of this vortical structure appears to be relatively insensitive to Reynolds number of the jet provided that the jet momentum is high enough for the jet to penetrate the cross-flow. It is conjectured that the breakdown of the structure shortly downstream of the bending of the jet is due to interaction between the vortices and Kelvin-Helmholtz like instabilities. Horseshoe vortices are generated near the ground as the cross-flow moves around the jet. Vertical jet ejecting downwards – not interacting with the groundA jet flame directed vertically downward will be shorter than if it was ejecting upwards, if buoyancy is taken into account and the jet does not interact with the ground. Horizontal free jetBuoyancy forces eventually exceed the momentum forces of the jet, and the flame tip rises. Co-flowing wind would make the jet longer, delaying the rise of the flame tip due to buoyancy. Horizontal jet near groundThere will be jet-ground interaction which will affect the flame length. Co-flowing wind would make the jet longer, while an opposing wind would reduce the flame length Lifted flamesJet flames with relatively low exit velocity will be stabilised on or attach to the nozzle exit. The diffu-sion flame sheet will become stretched and finally distorted if a critical exit velocity is exceeded and the flame will be stabilised some distance, the lift-off height, downstream of the nozzle exit. The lift-off height increases with increasing jet exit velocity, until a critical velocity has been reached at which point the flame is blown out. A lifted flame will re-attach to the nozzle if the exit velocity is reduced, but the re-attachment velocity will almost certainly be different from the lift-off velocity due to the hysteresis effect. Four different mechanisms have been proposed as explanation of the lift-off phenomenon:
Flame quenching is the probable mechanism responsible for lift-off of an initially attached flame, Peters (2000). Kalghatgi (1981) proposed a correlation to calculate the flame lift-off height based on maximum lami-nar flame speed. Kalghatgi (1981) also proposed a correlation to estimate the blowout velocity for hydrocarbon fuels for burners with different diameters: U_b = C_b S^2_{b,max} r_{jet},
where C_b is an experimental constant, S_{b,max} is the maximum laminar flame speed and r_{jet} is the radius of the burner. Eickhoff, H., Lenze, B., and Leuckel, W., Experimental investigation on the stabilization mechanism of jet diffusion flames, Twentieth Symposium (International) on Combustion, The Combustion Insti-tute, Pittsburgh, Pennsylvania, USA, 1984. Stable lifted flames and blow-out phenomenonStableLiftedFlamesAndBlow-outPhenomenon Jet fires in congested environment, effect of delayed ignitionJetFiresInCongestedEnvironmentEffectOfDelayedIgnition Pecularities of gas firesFree jet laminar and turbulent diffusion flamesFreeJetLaminarAndTurbulentDiffusionFlames Triple flamesTripleFlames Combustion of inhomogeneous mixture in closed vessel and pressure buildupCombustionOfInhomogeneousMixtureInClosedVesselAndPressureBuildUp Numerical models for combustion simulationEddy Break-up modelEddyBreak-upModel Flame Surface Density ModelsFlameSurfaceDensityModels The G-equation modelTheG-equationModel |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||