
|
BRHS /
Gas FireLaminar diffusion flamesBurke-Schumann flame structure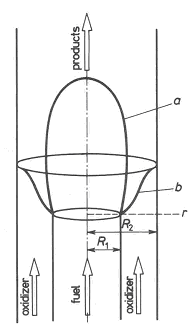 Figure 1. The shapes of laminar diffusion flame under: a) over- and b) underventilated situations [Chomiak 1990] Diffusion flames are when the fuel and oxidizer are physically separate so that the energy release rate is limited primarily by the mixing process. There is no fundamental flame speed as in the case of premixed flames. Chemical kinetics plays a secondary role. Diffusion flames occur with flowing gases, with vaporization of liquid fuels and with devolatilization of solid fuels. It follows from the experimental data that the reaction zone in diffusion flames is thin, just as in premixed flames, and can be treated as flame front. The flame front is located where the stream of the original components flowing into the combustion zone meet in a stoichiometric ratio. A classical example of a laminar diffusion flame, which was first described quantitatively by Burke and Shumann, is provided by a system in which fuel and air flow with the same linear flow velocity in coaxial cylindrical tubes. The observed shapes of diffusion flames may be divided into two classes. If the ratio of the dust radii rs top rj is such that more air is available than what is required for complete combustion, than an overventilated flame is formed and the flame boundary converges to the cylinder axis. On the other hand, if the air supply is insufficient for complete burning, than underventilated flame is produced in which the flame surface expands to the outer tube wall (Figure 1). The flame shapes and flame heights calculated from Burke and Shumann theory are in good agreement with experiments. Figure 2 shows some of the computed profiles and experimental data points. 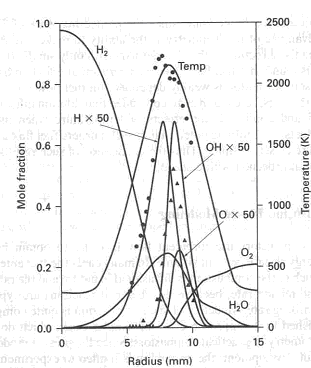 Figure 2. Concentration and temperature profiles in a hydrogen-air diffusion flame at 2 cm above fuel inlet; the hydrogen tube had a 5 cm radius; circles are measured temperatures and triangles are measured OH concentrations [Fukutani et al. 1991] Chomiak J. (1990) Combustion. A Study in Theory, Fact and Application. Gordon and Breach Science Publishers Turbulent diffusion flamesTurbulent diffusion jet flame: flame structure, specific features; scales and combustion regimes in turbulent non-premixed combustionThe diffusion is the rate-controlling process in turbulent diffusion flames. The characteristic time scales for convection and diffusion are normally much larger than the characteristic time scale of the combustion processes. The assumption of infinitely fast chemistry, or local chemical equilibrium, is therefore justified in some cases. This means that the modelling can be significantly simplified. However, there are situations where the assumption of fast chemistry does not hold, i.e. reactions involving CO and NOx, where the finite rate chemistry must somehow be represented. Local quenching, lift-off and blow-off can occur when the local diffusion time scale is of the same order of magnitude as that of the chemical timescale of the reactions. The assumption of local chemical equilibrium makes it possible to predict the flame length of a jet flame. Central to this is the introduction of mixture fraction, a conserved scalar, which is independent of chemistry. All scalars, such as density, temperature, species concentrations, are uniquely related to the mixture fraction. Combustion regimes There are four regimes in non-premixed turbulent combustion
For large mixture fraction fluctuations, Z'_{st} > (\Delta Z)_f , a regime of separated flamelets exists. The reaction is connected when Z'_{st} < (\Delta Z)_f , i.e. when the mixture fraction fluctuation is smaller than or equal to the diffusion thickness in mixture fraction space. Relationship between flame height and fuel flow rateLaminar diffusion flames: L \sim \dot{m}_{fuel}Hottel and Hawthorne (1949) suggested that a hydrogen-fuelled flame would undergo transition from laminar to turbulent flow at a Reynolds number of around 2000. Flame length is defined as the distance between the nozzle exit and the point on the jet centreline whe-re the mean mixture fraction equals the stoichiometric mixture fraction. Axisymmetric jet ejecting vertically upward – \frac{L + x_0} {d} = \frac {5.3} {Z_{st}} \left( \frac{\rho_0}{\rho_{st}} \right)^{1/2},
where x_0 is the virtual origin, d is the jet diameter, Z_{st} is the stoichiometric mixture fraction, \rho_0 is the ambient density and \rho_{st} is the density of a stoichiometric mixture. Peters and Göttgens (1991) presented a relation between a non-dimensionless flame length and the Froude number for buoyant diffusion flames. Peters (2000) included a graph showing the flame length against Froude number for propane-air diffusion flames. Vertical jet ejecting upwards – quiescent ambient conditionsThe flame will be longer if the jet is ejecting vertically upwards and buoyancy is taken into account. Vertical jet ejecting upwards – crosswind ambient conditionsThe momentum of the crosswind will cause the flame to bend over with the wind. Even a crosswind with relatively low momentum would make a high momentum jet bend over. Muppidi and Mahesh (2005) used DNS to simulate high momentum jets in a low momentum cross flow; A jet with a mo-mentum ratio of 1.5, Mjet/Mcrossflow, would be deflected at y/d \lambda 1.5 and a jet with a momentum ratio of 5.7 would be deflected at y/d \lambda 6. The jet will exhibit the characteristic kidney-shape due to counter-rotating vortices, which draws ambient air into the jet. The mechanism responsible for the formation of this vortical structure appears to be relatively insensitive to Reynolds number of the jet provided that the jet momentum is high enough for the jet to penetrate the cross-flow. It is conjectured that the breakdown of the structure shortly downstream of the bending of the jet is due to interaction between the vortices and Kelvin-Helmholtz like instabilities. Horseshoe vortices are generated near the ground as the cross-flow moves around the jet. Vertical jet ejecting downwards – not interacting with the groundA jet flame directed vertically downward will be shorter than if it was ejecting upwards, if buoyancy is taken into account and the jet does not interact with the ground. Horizontal free jetBuoyancy forces eventually exceed the momentum forces of the jet, and the flame tip rises. Co-flowing wind would make the jet longer, delaying the rise of the flame tip due to buoyancy. Horizontal jet near groundThere will be jet-ground interaction which will affect the flame length. Co-flowing wind would make the jet longer, while an opposing wind would reduce the flame length Lifted flamesJet flames with relatively low exit velocity will be stabilised on or attach to the nozzle exit. The diffu-sion flame sheet will become stretched and finally distorted if a critical exit velocity is exceeded and the flame will be stabilised some distance, the lift-off height, downstream of the nozzle exit. The lift-off height increases with increasing jet exit velocity, until a critical velocity has been reached at which point the flame is blown out. A lifted flame will re-attach to the nozzle if the exit velocity is reduced, but the re-attachment velocity will almost certainly be different from the lift-off velocity due to the hysteresis effect. Four different mechanisms have been proposed as explanation of the lift-off phenomenon:
Flame quenching is the probable mechanism responsible for lift-off of an initially attached flame, Peters (2000). Kalghatgi (1981) proposed a correlation to calculate the flame lift-off height based on maximum lami-nar flame speed. Kalghatgi (1981) also proposed a correlation to estimate the blowout velocity for hydrocarbon fuels for burners with different diameters: U_b = C_b S^2_{b,max} r_{jet},
where C_b is an experimental constant, S_{b,max} is the maximum laminar flame speed and r_{jet} is the radius of the burner. Eickhoff, H., Lenze, B., and Leuckel, W., Experimental investigation on the stabilization mechanism of jet diffusion flames, Twentieth Symposium (International) on Combustion, The Combustion Insti-tute, Pittsburgh, Pennsylvania, USA, 1984. Stable lifted flames and blow-out phenomenonObservations of high-momentum jet fires reveal that the base of the flame oscillates backwards and forwards in space. The flame will be blown out should the turbulent timescale be much smaller than the timescale associated with the chemical reactions. A re-ignition of the jet further downstream can-not be ruled out, though this is dependent on the availability of an ignition source. Broadwell et al. (1984) put forward an expression to predict blowout velocity of hydrocarbon-air mix-tures: (U_b)_{mix} = (U_b)_{fuel} \left[ \left( \frac{(S_{b,max})_{mix}}{(S_{b,max})_{fuel}} \right)^2 \left( \frac{(Y_{max})_{mix}}{(Y_{max})_{fuel}} \right)^2 \left( \frac{(\rho)_{mix}}{(\rho)_{fuel}} \right)^{1/2}\right],
where (U_b)_{fuel} is the blowout velocity for pure fuel, (S_{b,max})_{mix} is the maximum laminar flame speed for the mixture, (S_{b,max})_{fuel} is the maximum laminar flame speed for pure fuel, Ymax,mix is the ratio of fuel air mass fraction corresponding to the maximum flame speed for the mixture, Ymax,fuel is the ratio of fuel air mass fraction corresponding to the maximum flame speed for the fuel, and and are the densities of the mixture and pure fuel, respectively. Broadwell et al (1984) proposed that flame blow-out occurs when the ratio between the local mixing time and characteristic chemical timescale is less that a certain critical threshold. The expression yielded poor agreement with observed blowout ve-locities for hydrogen-air mixtures. It is possible to predict the blowout behaviour of a jet from calculations of the local velocities of a cold isothermal jet mixing, Choudhuri and Gollahalli (2000). Broadwell, J. E., Dahm, W. J. A., and Mungal, M. G., Blowout of turbulent flames, 20th Symposium (International) on Combustion, Combustion Institute, Pittsburgh, PA, USA, pp. 303-310, 1984 Jet fires in congested environment, effect of delayed ignitionJet fires occurring in congested environment will impinge on process equipment, structural members, etc. The potential for escalation is very real if the integrity of the structure is compromised; this could be brought on by the effects of heat transfer or by the impact of high jet momentum. The situation could be further complicated if there is a delay in the ignition of the fuel, because a cloud consisting of fuel and air with a concentration in the flammable range could be formed, thus increasing the possibility of an explosion. Pecularities of gas firesFree jet laminar and turbulent diffusion flames Figure 1. Free jet diffusion flame transition from laminar to turbulent flow (HottelHC:1949). Consider a gaseous fuel jet upward from a nozzle of diameter dj into stagnant air as shown in Figure 1. As the velocity of the fuel jet is increased, the character of the flame changes. At low jet velocity the mixing rate is slow and the flame is long and smooth (laminar). The laminar flame height increases linearly with jet velocity up to a point where the flame becomes turbulent. The flame height decreases due to more rapid turbulent mixing. In the stable, fully developed turbulent region, the flame height is independent of jet velocity. The transition to a fully developed turbulent flame may be characterized by a transition Reynolds number given in Table 1 (HottelHC:1949). As the jet velocity is further increased, a point is reached where the flame lifts off from the nozzle and exhibits a nonburning region at the bottom. A further increase in jet velocity causes the flame to blow off completely. Table 1. Jet diffusion flame transition to turbulent flow [Hottel and Hawthorne 1949]
In engineering practice, it is very useful to obtain quick solution by phenomenological analyses. Such simple approach gives the following dependence of the laminar diffusion jet flame height on the fuel volumetric flow rate \dot{V} and mass diffusivity D (KuoKK:2005): z_{f,L} \propto \frac{\dot{V}}{D}.
More fundamental approach gives following expressions for the flame radius at any particular z station and flame length (KuoKK:2005) r_{f} = z\frac{16}{\sqrt{3} Re_{d_{0} } } \sqrt{\sqrt{\frac{3}{16} \frac{Re_{d_{0} } r_{0} }{z f_{st} } -1} },
z_{f} = r_{0} \frac{3}{16} Re_{d_{0} } \left[ 1 + \frac{1}{ \left({F / O)_{st} Y_{O,A}} \right) } \right],
Re_{d_{0} } \equiv \frac{u_{0} d_{0} }{\nu } , f_{st} =\frac{\left(F/O\right)_{st} Y_{O,A} }{1+\left(F/O\right)_{st} Y_{O,A} },
where: r0, d0 - radius and diameter of fuel jet at the exit, respectively, u0 - fuel velocity at the exit, YO,A - mass fraction of the oxidizer in the ambient gas, (F/O)st - stoichiometric fuel to oxidizer ratio. Turbulent diffusion flame height is observed to be independent of the fuel volumetric feed rate but linearly dependent upon the nozzle diameter. Hottel H.C. and Hawthorne W.R. (1949) Diffusion in laminar flame jets. In Proceedings of the Third Symposium (International) on Combustion. Baltimore. Williams and Wilkins, pages 253-266.(BibTeX) Triple flamesExistence of triple flames can explain the flame stabilisation mechanism behind lifted diffusion fla-mes, Chen (2004). A triple flame consists of curved premixed flame front spanning lean to rich fuel composition along the stoichiometric mixture fraction contour with a trailing diffusion flame formed from the excess fuel and oxidiser in the premixed branches, Chen (2004). Ruetsch et al. (1995) showed that the heat release rate enhances the flame propagation speed. Echekki and Chen (1998) and Im and Chen (1999) explored the effects of heat release, preferential and differential diffusion and chemistry; these studies indicated that heat release was most important parameter in the enhancement of the flame propagation speed. Preferential diffusion accounts for less than 10 % of the flame speed enhancement near the leading edge, but the flame structure is greatly influenced by flame curvature and H2 and the H-radical at the triple point. Chen and Echekki (2000) studied buoyancy effects in triple flames. Chen and Echekki (2000) con-cluded that buoyancy and heat release have pronounced effect on the flame propagation velocity. The flame shape is significantly affected by buoyancy and the direction of the gravity vector. Chen, J. H., 2004. Combustion of inhomogeneous mixture in closed vessel and pressure buildupThe pressure will build up if a fire occurs in a closed vessel. This is due to the fact that the hot gases expand and no venting can take place. The combustion will be incomplete, leading to an increased production of CO as the available oxygen is consume, until the oxygen has become depleted after which combustion will cease. Simple combustion models are not well equipped to deal with inhomo-geneous mixtures, while models utilising detailed or reduced chemical kinetics are more appropriate. |