
|
BRHS /
Transition from deflagration to detonationDDT basicsPhenomenology of flame acceleration and deflagration to detonation transitionThe sequence of events leading to detonation in a tube containing explosive gases can be summarized as follows:
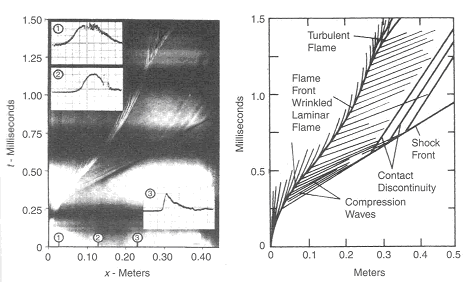 Figure 1a. The development of detonation in stoichiometric H2-O2 mixture initially at normal temperature and pressure, showing the generation of pressure waves ahead of the accelerating flame. 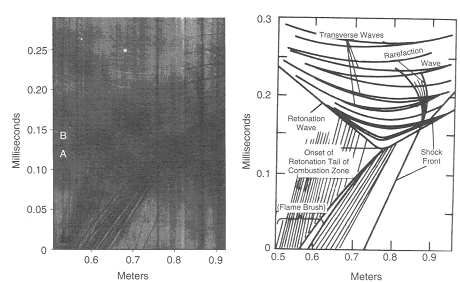 Figure 1b. The onset of retonation. For both photographs spark ignition by discharging 1.0 mJ. Electrodes located at closed end of 25 x 37 mm cross-section tube (Oppenheim et al., 1963). Streak schlieren photographs. The forward-mowing wave was studied using wall imprints of the detonation process, an example of which is shown in Fig. 3. The characteristic fish-scale pattern, which corresponds to inception of the forward shock, is a distinguished feature of a self-sustained detonation front. There are generally four different modes of transition process observed and classified, based on the location of the onset of an “explosion in an explosion”: between flame and shock front (Fig.4a), at the flame front (Fig.4b), at shock front (Fig.4c) and at the contact discontinuity (Fig.4d). The oset of detonation depends on the particular pattern of shock fronts created by the accelerating flame. The process of DDT is unreproducible in its detailed sequence of events. DDT refers to the phenomena where the critical conditions for the onset of detonation are established by the combustion process itself without external energy source. There are several ways by which the conditions necessary for transition can be achieved. These include:
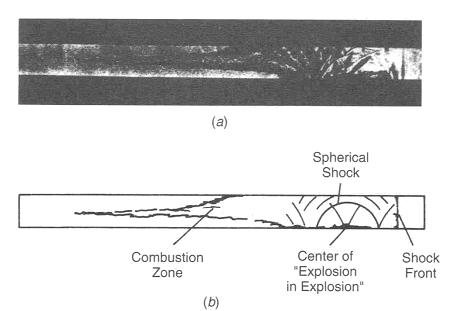 Figure 2. Flash schlieren photograph of the onset of retonation in a stoichiometric H2-O2 mixture initially at normal temperature and pressure at an instant marked by A on streak schlieren photo (Fig.1)(Oppenheim et al., 1963).  Figure 3. Wall imprints of the transition process.  Figure 4. Various modes of DDT observed in 2H2+O2 mixture; a) onset occurring between flame and shock, b) onset occurring at flame front, c) onset occurring at shock front, d) onset occurring at contact discontinuity. (Urtiew and Oppenheim, 1966). Effect of chemical composition, pressure, temperature, geometry, and system physical scaleEffect of non-uniformity (SWACER) In DDT process energy required to initiate detonation is provided by rapid release of energy during combustion to produce a blast wave of sufficient strength to cause detonation. As described by Lee (LeeJHS:1980), such shock waves can be produced by prescribing a spatial and temporal coherence of the energy release. Theoretically, the required coherence can be achieved by pre-conditioning the explosive mixture so that the induction time \tau increases in a prescribed manner away from an initial ignition point to produce energy source which propagates at a velocity V_0 = (\partial \tau /\partial x)^{-1} . Spatial gradients in induction time are due to gradients in temperature and/or free radical concentrations. The so-called SWACER (Shock Wave Amplification by the Coherent Energy Release) mechanism was first proposed to account for photochemical initiation in H2-Cl2 mixtures. Gradients in temperature and free radicals are also produced by turbulent mixing of hot combustion products with unburned gas in turbulent eddies associated with flame propagation around obstacles or in turbulent flame jets. Knystautas et al. (KnystautasR:1979) achieved DDT by injecting a hot turbulent jet into a quiescent fuel-oxygen mixture. Coherent energy release by itself is not enough for DDT, the volume of coherent energy release must be also be large enough to produce a strong enough shock wave with long enough duration to initiate detonation in the surrounding unburned mixture. A lower bound of the volume required for transition to occur in an unconfined cloud can be obtained by equating the chemical energy in a spherical volume to the critical initiation energy by an external source: E_{c} =\frac{\pi \rho _{0} QD_{c}^{3} }{6}
where Q is the chemical energy release per unit volume, \rho_0 is the density of the unburned mixture, and D_c is the critical explosion diameter. Lee J.H.S. and Moen I. O. (1980) The mechanism of transition from deflagration to detonation in vapor cloud explosions. Progress in Energy Combustion Science, 6:359-389.(BibTeX) Criteria for spontaneous flame acceleration to supersonic flame speed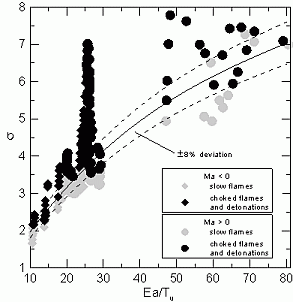 Figure 1. Observed combustion regime as a function of expansion ratio \sigma and dimension- less activation energy Ea/RTu for hydrogen-air and hydrocarbon-air mixtures for closed systems. Picture reproduced with permission from (DorofeevSB:2001). The next phenomenon which strongly influences the route of combustion process is flame acceleration. As it was shown in (DorofeevSB:2001), the possibility of flame acceleration is defined by mixture properties. The experimental data on the combustions in confined volumes from a wide variety of test facilities with the different characteristic lengths and the geometric configurations were analyzed. The analysis showed that strong flame acceleration was observed only for the sufficiently sensitive mixtures (Figure 1). The parameter, which controls the possibility of flame acceleration, was identified as an expansion ratio \sigma (ratio between density of unburned and burned mixture at constant pressure). An expression of critical expansion ratio (below which the flame acceleration is not observed) reads as \sigma^* = 0.9 \times 10^{-5} \cdot x^3 - 0.0019 \cdot x^2 + 0.1807 \cdot x + 0.2314, \ \ \ \ \ (1)
where x is dimensionless activation energy x = Ea/RTu . For hydrogen-air mixtures this parameter is approximately equal to 25 and, therefore, for critical value \sigma^* gives approximately value of 3.7. In case of systems with partial transverse venting (as it was shown in [4], see Figure 2) the critical value \sigma^* is modified proportionally to vent ratio \alpha (ratio between surface of vent and surface of enclosure). The larger is the vent area the more reactive mixtures is necessary for development of fast flames. The resulting expression for critical expansion ratio reads as \sigma_{cr} = \sigma^* \cdot (1 + 2.24 \cdot \alpha)
where \sigma^* is critical expansion ratio for closed systems (Eq. (1)). On the basis of findings of [(DorofeevSB:2001), (AlekseevVI:2001)], it is possible to formulate a criterion for strong flame acceleration: the mixture can exhibit strong flame acceleration only if its expansion ratio is larger than critical expansion ratio \sigma^{cr} . This statement has to be supplemented with the following: strong flame acceleration can take place only if there is enough room for actual development of supersonic flame. This geometric limitation is connected with necessity of run-up distance for flame acceleration process, which can be evaluated for tube-like configurations as having value of 20-40 diameters (see, e.g., [5]). Such formulated criterion has a character of necessary condition and thus can be directly used for evaluation of flame acceleration potential in CFD simulations. 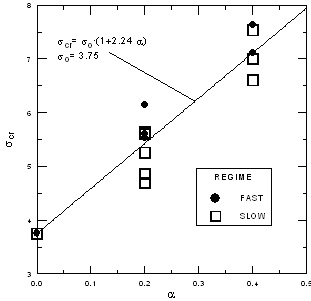 Figure 2. Observed combustion regime as a function of expansion ration \sigma and vent ratio\alpha . Dependence of critical expansion ratio \sigma^{cr} on \alpha . Picture reproduced with permission from (AlekseevVI:2001). Note, that the proposed criterion has, unfortunately, only limited range of applicability, since it was deduced on the basis of data obtained in confined and confined with partial venting systems. The generalization of this criterion to lower degrees of confinement and to open systems should provide extremely useful information for evaluation of flame acceleration potential in safety analysis. Dorofeev S.B., Kuznetsov M.S., Alekseev V.I., Efimenko A.A. and Breitung W. (2001) Evaluation of limits for effective flame acceleration in hydrogen mixtures. Journal of Loss Prevention in the Processes Industries, 14:583-589.(BibTeX) Criteria for establishment of stable detonationOne of the most important critical event, which can strongly affect the regime of combustion, is deflagration-to-detonation transition. For many years many efforts was being made to develop a theory of this event, however it is still far from complete understanding. Due to this fact, the DDT predictions from CFD simulations hardly can have reliable character. To avoid uncertainty in forecast of DDT a criterion for detonation onset was proposed. 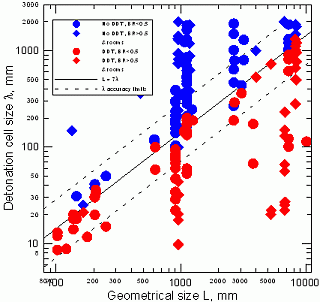 Figure 1. Critical conditions for onset of detonations in rooms and channels with obstacles. Deviations from line L = 7\lambda are within 30%. Picture reproduced with permission from (DorofeevSB:2000). For systematization of conditions in which DDT event can take place, numerous sources of data were analyzed in (DorofeevSB:2000). The literature data and the data from experiments carried out by authors were used. It was shown that depending on geometry of the facility, the mixture of the same composition can exhibit different behavior. In the facilities with characteristic length large than certain value (defined by mixture reactivity) the mixture does detonate, and in smaller facilities the detonation does not occur. The results of analysis are summarized in Figure 1. Solid line L = 7\lambda separate analyzed cases with observed detonation from cases without detonation onset. As it was indicated by authors an accuracy of such separation is within 30% of \lambda value. Parameter \lambda, which is used as characteristic length for characterization of mixture sensitivity, is detonation cell size. Detonation cells are imprint of complex three-dimensional structure of detonation wave and their size is determined by mixture properties only (e.g., H2 concentration, initial temperature) and does not depend on geometric configuration of detonating mixture. The values of detonation cells are often known only with inaccuracy of 100%, therefore an application of 7\lambda correlation has to be made with understanding of accuracy of this correlation. A criterion built on basis of 7\lambda correlation reads as: for detonation onset to be possible a characteristic size of combustible mixture (cloud or room size) must exceed 7\lambda (necessary condition). If detonation develops as a transition from fast deflagration, the corresponding criterion for flame accelleration has to be fulfilled as well. Note that this criterion as well as criterion for flame acceleration has limited character of applicability since for non-uniform mixtures with spatially dependent properties (e.g., concentration) assessments of detonation cell size and expansion ratio can have considerable uncertainties in their values. However, by the moment these criteria provide the most reliable methodic on the potential of flame acceleration and DDT events. Dorofeev S.B., Sidorov V.P., Kuznetsov M.S., Matsukov I.D. and Alekseev V.I. (2000) Effect of scale on the onset of detonations. Shock Waves, 10:137-149.(BibTeX) Transition to detonation during venting of hydrogen deflagrationsSWACER mechanism<< | Content | >> |