• View
• Edit
• History
• Print

Potential For Accumulation Depending On Leaking

When the jet or buoyant plume is established within the enclosure, the medium-term atmosphere conditions would be either well-mixed or inhomogeneous. The relevant phenomena are:

1. local accumulation on dead-end regions
2. stratification-homogenisation in ceilings
3. homogenisation by convective motions
4. venting phenomena
5. mitigation systems

Local accumulation usually happens in regions near the release point or in the way of circulation loops. There are regions in the enclosure with dead-end enclosures, badly-vented or ceiling, which make difficult the ascending dispersive motions.

Stratification-homogenisation in ceilings is a more complex phenomenon. The stratification consists on forming stable layers of fluid which do not mix each other, because of the lack of atmosphere gradients apart from jets, plumes or boundary layers. When stratification happens the fluid is not stagnated, but the motion does not allow mixing between separate layers.

The mixing patterns established in the enclosure are induced by jets, plumes and convective heat transfer. These phenomena induce moments in the fluid, which produce the competition between two forces: inertia and buoyancy. When the inertia forces are dominant, the enclosure atmosphere will get mixed. When buoyancy is prevailing the stratification remains, and in this case the vertical gradient is established as a balance of ((WoodcockJ:2001)):

1. thermo-hydrodynamic stability (by temperature gradients)
2. horizontal fluxes (by air entrainment)
3. ceiling plumes (by Rayleigh-Bénard convective motions)

The thermo-hydrodynamic stability is diagnosed characterised by the Richardson number, Ri,

and the Reynolds number

where being H the enclosure height, u_e the entrainment velocity and μ₀ the dynamic viscosity at the break point. When Richardson number is higher greater than unity and greaterhigher than the inverse of the Reynolds number, buoyancy forces dominate inertia forces and the density gradients at the horizontal direction are negligible. From this condition, (PetersonPF:1994) established criteria for stratification in a confined environment (bounded at the upper part, but open in transversal directions to avoid accumulation).

In the case of a round jet, stratification happens occurs when the following criterion is satisfied:

as demonstrated by Lee et al. (LeeJH:1974) and Jain and Balasubramanian (BalasubramanianV:1979) (Fig. 1).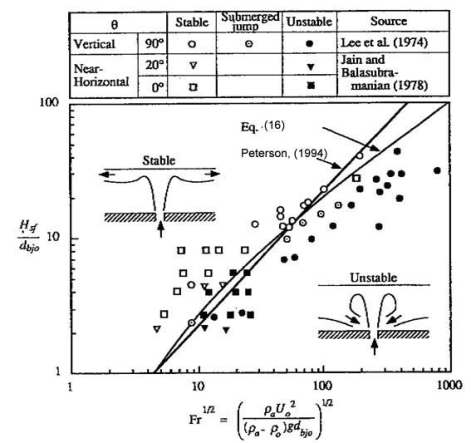

Fig. 1: Stratification criteria for round jets (PetersonPF:1994)

In case of a round buoyant plume, the criterion is the following

These criteria are not conditions sufficient to quantify the buoyancy gradients. It is necessary to analyse other effects in order to establish mixing or stratified conditions in enclosures: horizontal fluxes and ceiling plumes. The Rayleigh number, Ra, which is defined as

is used in this case to determinate these conditions. When this dimensionlessthe Rayleigh number is greaterhigher than 109, the turbulent fluxes generate density gradients which reduce the stability of the stratified layers, and poses initiates mixing patterns (WoodcockJ:2001).

Finally, the location of the release point could reduce established inhomogeneous conditions in a closed room, by the fact that the inertia forces are not enough to impulse the hydrogen below the release point. Then hydrogen will accumulate at the upper part of the room and the mixing process will be led by slower phenomena: molecular diffusion or convective heat. Some experiments as NUPEC M-8-1 (CSNI:1999) and Shebeko (ShebekoYN:1988) have illustrated this phenomenon.

References

Invalid BibTex Entry!

<< Molecular versus Turbulent Mixing | Content | Influence of Natural Ventilation of Structures >>