
|
BRHS /
Flame stretch and effect of flame curvature, Markstein lengthsFlame front propagation in a non-uniform flow is affected by strain and curvature effects, which lead to the change in the flame area and measured by flame stretch, which is a fractional rate of change of a flame surface element: k = \frac{1}{A}\frac{{dA}}{{dt}},
where k \ - flame stretch, A – area of the flame surface element, t - time. Asymptotic theories, e.g. (MarksteinGH:1964), (WilliamsFA:1985), (ClavinP:1985) suggest that the flame stretch (flame strain, or flame curvature, or both) may affect the laminar burning velocity and in the limit of the small stretch it controls the laminar burning velocity through the linear relationship: s_u = s_{u\infty } - L\,k, \ \ \ \ \ \ \ \ (1)
where s_u - laminar burning velocity, s_{u\infty } - laminar burning velocity of planar unstretched flame, L – Markstein length, k - stretch rate. The above expression is often recast in the following form: \frac{{s_u }}{{s_{u\infty } }} = 1 - Ma \cdot \frac{{k\delta }}{{s_{u\infty } }} = 1 - Ma \cdot Ka , \ \ \ \ \ \ \ \ (2)
where Ma=L/\delta - Markstein number, \delta = {{\lambda _u } / {\left( {\rho _u \,c_p s_{L\infty } } \right)}} - characteristic flame front thickness, Ka = k \delta / s_{u\infty } - Karlovitz number. Formally a linear dependence between the burning velocity s_u and the stretch rate k , which is a result of a theoretical analysis, is valid only for small stretch rates ( Ka << 1 ). In fact, a non-linear relationship between and k is found for a broader range of k (AungKT:1997). 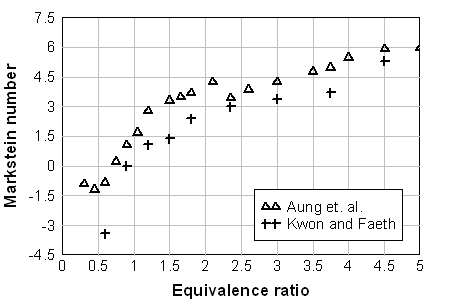 Fig. 1. Markstein number of the hydrogen-air flame at normal pressure and temperature as a function of the equivalence ratio \Phi . (AungKT:1997), (KwonOC:2001). The sign of the Markstein length (Markstein number) controls the preferential-diffusion stability of the laminar flame fronts. Equations (1), (2) readily demonstrates the relationship between the stretch and preferential-diffusion instability: if the Markstein length (Markstein number) is negative then the laminar burning velocity increases as the flame stretch increases. This causes bulges in a flame front with a positive stretch to grow further and thus the flame is unstable. If the Markstein number is positive, then the laminar burning velocity decreases with increasing stretch and similar bulges in the flame surface become smaller, so that flame become stable to preferential-diffusion instability. Hydrogen flames are unstable in learn mixtures. Figure 1 shows the Markstein number of H2-air flames as a function of the equivalence ratio \Phi ; at normal temperature and pressure reported in (AungKT:1997) and (KwonOC:2001). The neutral preferential-diffusion condition is at equivalence ratio \Phi=0.7-0.9 . With increase of pressure the Markstein length L becomes positive at larger equivalence ratios (KwonOC:1992), (TseSD:2000). Markstein length of H2-air flames was reported in (DowdyDR:1990), where it changed from about –0.4 mm at \Phi=0.3\ (~10% H2) and up to 0.5 mm at \Phi=2.3\ (~68%). Poinsot T. and Veynante D. (2001) Theoretical and numerical combustion. Edwards, Philadelphia.(BibTeX) << Dependence of laminar burning velocity on mixture composition, pressure and temperature | Content | Flame cellular structure and wrinkling >> |