
|
BRHS /
Laminar burning velocity and laminar flame thicknessLaminar flames propagate via the diffusion of heat and free radicals from the reaction zone to the unburned mixture ahead of it to effect ignition. The diffusion flux depends on the temperature gradient (which in turn depends on the reaction rate) and the various transport coefficients for the different species. The pressure remains practically constant across a laminar flame, hence the flame temperature corresponds closely to the product temperature for a constant pressure adiabatic process. The quantitative description of a laminar flame requires a detailed knowledge of the chemical kinetics, transport coefficients, and the thermochemical data of the various chemical species involved in the reactions. Thus, the laminar burning velocity provides a fundamental parameter whereby one can assess one's knowledge of the combustion process of a given explosive mixture. There are various methods for the experimental measurement of the laminar burning velocity but each has certain advantages and disadvantages. 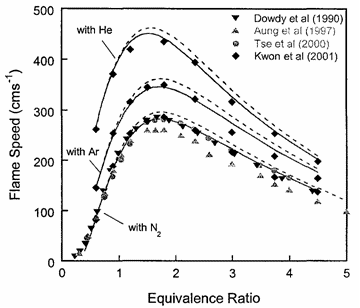 Figure 1. Laminar flame speed at 298 K and 1 atm for \mathrm{H_2}-\mathrm{O_2} mixed with \mathrm{N_2}, \mathrm{He} and \mathrm{Ar} (\mathrm{O_2}:\mathrm{N_2} = \mathrm{O_2}:\mathrm{He} = \mathrm{O_2}:\mathrm{Ar} = 1:3.76). From Lee (2006) (LeeJHS:2006). The solid and dashed lines are predicted values obtained with chemical kinetic mechanisms. Since the laminar burning velocity depends on curvature and flow straining, the correct laminar burning velocity is often difficult to determine. Flame instability also adds to the difficulty of the experimental measurement of the laminar burning velocity especially in the composition range where the flame is cellular. Theoretical computation of the laminar burning velocity is possible provided that the flame chemistry, transport coefficients and the thermochemical data are known. There are standard computer codes (e.g. CHEMKIN) available for such purposes. In general, the weakest link is usually associated with the inadequate modelling of the detailed flame chemistry. In fact, experimental burning velocity data is used to validate theoretical models of the detailed flame chemistry. For hydrogen-oxygen mixtures, the flame chemistry is perhaps the most well-established compared to the other common hydrocarbon fuels. A comparison between theoretical and experimentally measured values is given in Figure 1 for hydrogen-oxygen mixtures using various inert diluents (i.e. argon, helium, and nitrogen). The excellent agreement indicates that the chemistry of hydrogen-oxygen flames is now quite well-established. In Figure 1 it is also seen that the maximum laminar burning velocity for hydrogen-oxygen-nitrogen (or -air) mixtures is about 300 cm/s which is approximately six times that of most of the common hydrocarbon fuels of the order of 40 cm/s. This is a result of the high diffusivity of hydrogen, accounting for the shift of the maximum burning velocity towards richer mixtures. For the common hydrocarbon fuels, the maximum burning velocity occurs at just slightly richer than stoichiometric composition. It should be noted that laminar flame models also provide the fundamental basis for the modelling of turbulent flames. Also, a good understanding of the flame chemistry is essential to the choice of inhibitors for the suppression of explosions. For hydrogen-oxygen mixtures the flame chemistry is adequately known (Lee (2006) (LeeJHS:2006)). The magnitude of the laminar burning velocity is determined experimentally. Techniques of measuring flame velocity may be categorised as folows:
The advantages and disadvantages of these methods have been described by Koroll, Kumar & Bowles (1993) (KorollGW:1993):
A rudimentary way to estimate the laminar flame thickness rests on the assumption thatflame propagation is driven by heat conduction only (PoinsotT:2001): \delta_L = \frac{\lambda_u }{\rho_u {C_\mathrm{P}}_u} \frac{1}{{S_u}_L}
Here \delta_L denotes the laminar flame thickness; \lambda_u, \rho_u and {C_\mathrm{P}}_u} respectively denote the thermal conductivity, density and specific heat of unburnt (fresh) mixture; and, {S_u}_L the laminar burning velocity. Estimates obtained in this manner have been found to underestimate the real flame thickness by a factor of five. Similar expressions to estimate the laminar flame thickness have also been proposed by Blint (1986) (BlintRJ:1986) (see pages 57 and 58 of Poinsot & Veynante (2001) (PoinsotT:2001)).  Figure 2. Definition of the laminar flame thickness. From Poinsot & Veynante (2001) (PoinsotT:2001). More accurate values for the laminar flame thickness may be obtained from the numerical solution of the governing equations applied to the flame structure. An example of flame thickness of hydrogen-air mixtures obtained in this manner is by Aung, Hassan & Faeth (1997) (AungKT:1997). These authors report the following magnitudes for the unstretched laminar flame thickness \delta_L^{\circ} at normal temperature and pressure: \delta _L^{\circ} = 0.65 mm for equivalence ratio \Phi = 0.40 ; \delta _L^{\circ} = 0.35 mm for \Phi = 0.70 and \delta _L^{\circ} = 0.43 mm for \Phi = 4.0 . The unstretched laminar flame thickness \delta_L^{\circ} is defined as follows (Poinsot & Veynante (2001) (PoinsotT:2001)) and illustrated by Figure 2: \delta_L^{\circ} = \frac{T_2-T_1}{\mathrm{max}\left(\left|\partial T/\partial x\right|\right)}
There is also another laminar flame thickness as illustrated by Figure 2: the total thickness \delta _L^{\scriptstyle \mathrm{t}} . This quantity is defined as the distance over which the reduced temperature \theta = (T - T_1)/(T_2 - T_1) changes from 0.01 to 0.99; but this quantity is not very useful for modeling purposes (Poinsot & Veynante (2001) (PoinsotT:2001)). Its definition creates a long temperature tail which does not correspond with the species profiles across the flame structure. Aung K.T., Hassan M.I. and Faeth G.M. (1997) Flame stretch interactions of laminar premixed hydrogen/air flames at normal temperature and pressure. Combustion and Flame, 109:1-24.(BibTeX) << Structure of the reaction zone and flame temperature | Content | Dependence of laminar burning velocity on mixture composition, pressure and temperature >> |